题目内容
13. 如图,下列式子不能说明点C是线段AB(AC>BC)的黄金分割点的是( )
如图,下列式子不能说明点C是线段AB(AC>BC)的黄金分割点的是( )| A. | $\frac{BC}{AC}$=$\frac{\sqrt{5}-1}{2}$ | B. | AC+BC=$\frac{\sqrt{5}-1}{2}$AB | C. | $\frac{AC}{AB}$=$\frac{\sqrt{5}-1}{2}$ | D. | AC2=AB•BC |
分析 根据黄金分割的概念和黄金比值判断即可.
解答 解:当$\frac{BC}{AC}$=$\frac{\sqrt{5}-1}{2}$时,点C是线段AB(AC>BC)的黄金分割点,A正确;
AC=$\frac{\sqrt{5}-1}{2}$AB时,点C是线段AB(AC>BC)的黄金分割点,B不正确;
$\frac{AC}{AB}$=$\frac{\sqrt{5}-1}{2}$时,点C是线段AB(AC>BC)的黄金分割点,C正确;
AC2=AB•BC时,点C是线段AB(AC>BC)的黄金分割点,D正确,
故选:B.
点评 本题考查的是黄金分割的定义:把线段AB分成两条线段AC和BC(AC>BC),且使AC是AB和BC的比例中项,叫做把线段AB黄金分割,点C叫做线段AB的黄金分割点,黄金比为$\frac{\sqrt{5}-1}{2}$.

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
18. 如图,已知线段AB长为10cm,C是线段AB上任意一点,则AC的中点与BC的中点之间的距离是( )
如图,已知线段AB长为10cm,C是线段AB上任意一点,则AC的中点与BC的中点之间的距离是( )
 如图,已知线段AB长为10cm,C是线段AB上任意一点,则AC的中点与BC的中点之间的距离是( )
如图,已知线段AB长为10cm,C是线段AB上任意一点,则AC的中点与BC的中点之间的距离是( )| A. | 3cm | B. | 4cm | C. | 5cm | D. | 不能确定 |
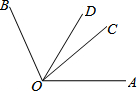 如图,已知∠COB=2∠AOC,OD平分∠AOB,且∠COD=23°,求∠AOB的度数.
如图,已知∠COB=2∠AOC,OD平分∠AOB,且∠COD=23°,求∠AOB的度数. 已知:如图△ABC中,AB=AC,∠C=30°,AB⊥AD,AD=5cm,求BC的长.
已知:如图△ABC中,AB=AC,∠C=30°,AB⊥AD,AD=5cm,求BC的长.