题目内容
3.已知$\left\{\begin{array}{l}{x-4y-5z=0}\\{-3x+y+4z≠0}\end{array}\right.$,且xyz≠0,则$\frac{xy}{{z}^{2}}$=-1.分析 把z看做已知数表示出方程组的解得到x与y,代入原式计算即可得到结果.
解答 解:方程组整理得:$\left\{\begin{array}{l}{x-4y=5z①}\\{-3x+y=-4z②}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=z}\\{y=-z}\end{array}\right.$,
∴$\frac{xy}{{z}^{2}}=\frac{-{z}^{2}}{{z}^{2}}=-1$,
故答案为:-1.
点评 此题考查三元一次方程组的解法,关键是把z看做已知数表示出方程组的解.

练习册系列答案
相关题目
14.为了准备6年后小颖上大学的学费20000元,她的父母现在参加了教育储蓄.有三种储蓄方式:
已知教育储蓄利率为一年期的年利率为2.25%,三年期的年利率为2.70%,六年期的年利率为2.88%.你认为哪种储蓄方式开始存入的钱较少?
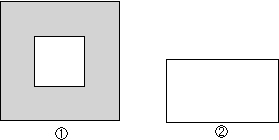
| 存入方式 | 内容 |
| 1 | 直接存入一个6年期 |
| 2 | 先存一个三年期,3年后将本息和自动转存一个三年期 |
| 3 | 先存一个一年期,然后每一年将本息和自动转存下一个一年期 |
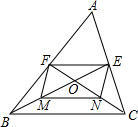 如图,BE,CF是△ABC的两条中线,它们相交于点O,M,N分别是OB,OC的中点,你能确定四边形FMNE是什么特殊四边形吗?请说明你的理由.
如图,BE,CF是△ABC的两条中线,它们相交于点O,M,N分别是OB,OC的中点,你能确定四边形FMNE是什么特殊四边形吗?请说明你的理由.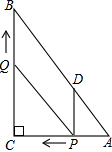 如图,在Rt△ABC中,∠C=90°,AC=6,BC=8,动点P从点A开始沿边AC向点C以每秒1个单位长度的速度运动,动点Q从点C开始沿边CB向点B以每秒2个单位长度的速度运动,过点P作PD∥BC,交AB于点D,连接PQ.点P、Q分别从点A、C同时出发,当其中一点到达端点时,另一点也随之停止运动,设运动时间为t秒(t≥0).
如图,在Rt△ABC中,∠C=90°,AC=6,BC=8,动点P从点A开始沿边AC向点C以每秒1个单位长度的速度运动,动点Q从点C开始沿边CB向点B以每秒2个单位长度的速度运动,过点P作PD∥BC,交AB于点D,连接PQ.点P、Q分别从点A、C同时出发,当其中一点到达端点时,另一点也随之停止运动,设运动时间为t秒(t≥0). 平原上有四个村庄A、B、C、D,为解决当地缺水是问题,政府准备投资修建一个蓄水池到四个村庄的距离之和最小,如图,蓄水池应该建在点P处,运用的数学道理是两点之间线段最短.
平原上有四个村庄A、B、C、D,为解决当地缺水是问题,政府准备投资修建一个蓄水池到四个村庄的距离之和最小,如图,蓄水池应该建在点P处,运用的数学道理是两点之间线段最短. 如图,PA切⊙O于A,PC交⊙O于B、C两点,M为$\widehat{BC}$的中点,AM交BC于点D.求证:PA=PD.
如图,PA切⊙O于A,PC交⊙O于B、C两点,M为$\widehat{BC}$的中点,AM交BC于点D.求证:PA=PD.