题目内容
5．
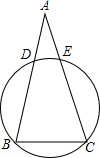如图，$\widehat{BD}$=$\widehat{CE}$，求证：AB=AC．
分析 先由$\widehat{BD}$=$\widehat{CE}$得到$\widehat{BE}$=$\widehat{CD}$，则根据圆心角、弧、弦的关系得到∠C=∠B，然后利用等腰三角形的判定即可得到AB=AC．
解答 证明：∵$\widehat{BD}$=$\widehat{CE}$，
∴$\widehat{BD}$+$\widehat{DE}$=$\widehat{CE}$+$\widehat{DE}$，
即$\widehat{BE}$=$\widehat{CD}$，
∴∠C=∠B，
∴AB=AC．
点评 本题考查了圆心角、弧、弦的关系：在同圆和等圆中，相等的圆心角所对的弧相等，所对的弦也相等．推论：在同圆或等圆中，如果两个圆心角、两条弧、两条弦中有一组量相等，那么它们所对应的其余各组量都分别相等．
练习册系列答案
相关题目
如图，将一张正方形铁片的4个角剪去4个大小一样的小正方形，然后折起来就可以制成一个无盖的长方体容器，设这个正方形铁片的边长为a，做成的无盖长方体容器高为h．
如图，在△ABC中，AB=AC，点O为AB边上一点，OA=2，OB=1，过点A作AD∥BC，且∠COD=∠B．求证：AD•BC=3．
如果所示，已知∠1=∠2，∠3=∠4，则下列结论正确的个数为（ ）