题目内容
10.已知实数x,y满足x+y=6,且x<7,y<2,若k=x-y,则k的取值范围是2<k<8.分析 首先解关于x和y的方程组,利用k表示出x和y,然后根据x<7,y<2即可列不等式组求得k的范围.
解答 解:解关于x和y的方程组$\left\{\begin{array}{l}{x+y=6}\\{k=x-y}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=\frac{k+6}{2}}\\{y=\frac{6-k}{2}}\end{array}\right.$.
根据题意得:$\left\{\begin{array}{l}{\frac{k+6}{2}<7}\\{\frac{6-k}{2}<2}\end{array}\right.$,
解得:2<k<8.
故答案是:2<k<8.
点评 本题考查了二元一次方程组和不等式组的解法,正确利用k表示出x和y的值是关键.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
相关题目
7. 小东同学在学习了二次函数图象以后,自己提出了这样一个问题:
小东同学在学习了二次函数图象以后,自己提出了这样一个问题:
探究:函数$y=\frac{1}{2}{(x-1)^2}+\frac{1}{x-1}$的图象与性质.
小东根据学习函数的经验,对函数$y=\frac{1}{2}{(x-1)^2}+\frac{1}{x-1}$的图象与性质进行了如下探究:下面是小东的探究过程,请补充完成:
(1)函数$y=\frac{1}{2}{(x-1)^2}+\frac{1}{x-1}$的自变量x的取值范围是x≠1;
(2)下表是y与x的几组对应值.
则m的值是$\frac{29}{6}$;
(3)如图,在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点,并画出该函数的图象;
(4)小东进一步探究发现,该函数图象在第一象限内的最低点的坐标是$(2,\frac{3}{2})$,结合函数的图象,
写出该函数的其他性质(一条即可):当x<1时,y随x的增大而减小.
 小东同学在学习了二次函数图象以后,自己提出了这样一个问题:
小东同学在学习了二次函数图象以后,自己提出了这样一个问题:探究:函数$y=\frac{1}{2}{(x-1)^2}+\frac{1}{x-1}$的图象与性质.
小东根据学习函数的经验,对函数$y=\frac{1}{2}{(x-1)^2}+\frac{1}{x-1}$的图象与性质进行了如下探究:下面是小东的探究过程,请补充完成:
(1)函数$y=\frac{1}{2}{(x-1)^2}+\frac{1}{x-1}$的自变量x的取值范围是x≠1;
(2)下表是y与x的几组对应值.
| x | … | -2 | -1 | 0 | $\frac{1}{2}$ | $\frac{2}{3}$ | $\frac{4}{3}$ | $\frac{3}{2}$ | 2 | 3 | 4 | … |
| y | … | $\frac{25}{6}$ | $\frac{3}{2}$ | $-\frac{1}{2}$ | $-\frac{15}{8}$ | $-\frac{53}{18}$ | $\frac{55}{18}$ | $\frac{17}{8}$ | $\frac{3}{2}$ | $\frac{5}{2}$ | m | … |
(3)如图,在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点,并画出该函数的图象;
(4)小东进一步探究发现,该函数图象在第一象限内的最低点的坐标是$(2,\frac{3}{2})$,结合函数的图象,
写出该函数的其他性质(一条即可):当x<1时,y随x的增大而减小.
 如图,正方形网格中的每个小正方形边长都是1,任意连接这些小正方形的顶点,可得到一些线段.
如图,正方形网格中的每个小正方形边长都是1,任意连接这些小正方形的顶点,可得到一些线段.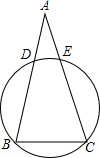 如图,$\widehat{BD}$=$\widehat{CE}$,求证:AB=AC.
如图,$\widehat{BD}$=$\widehat{CE}$,求证:AB=AC. 如图,AC⊥BC,垂足为点C,CD⊥AB,垂足为点D,则点A到BC的距离是线段AC的长度.
如图,AC⊥BC,垂足为点C,CD⊥AB,垂足为点D,则点A到BC的距离是线段AC的长度.