题目内容
13．已知实数a满足$\sqrt{a-2012}$+|2011-a|=a，那么a-20112=2012．分析 根据负数没有平方根，得到a-2012大于等于0，然后根据a的范围化简绝对值，移项后两边平方即可求出所求式子的值．
解答 解：∵负数没有平方根，
∴a-2012≥0，即a≥2012，
∴原式可化为：a-2011+$\sqrt{a-2012}$=a，即$\sqrt{a-2012}$=2011，
两边平方得：a-2012=20112，
解得：a-20112=2012．
故答案为：2012．
点评 本题考查的是非负数的性质以及二次根式有意义的条件，先根据题意求出a的取值范围是解答此题的关键．
练习册系列答案
阅读快车系列答案
相关题目
如图，正方形网格中的每个小正方形边长都是1，任意连接这些小正方形的顶点，可得到一些线段．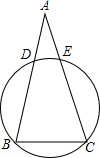
如图，$\widehat{BD}$=$\widehat{CE}$，求证：AB=AC．