题目内容
9.有5张看上去无差别的卡片,正面分别写着1,2,3,4,5,洗匀后正面向下放在桌子上,从中随机抽取2张,抽出的卡片上的数字恰好是两个连续整数的概率是$\frac{2}{5}$.分析 列表得出所有等可能的情况数,找出恰好是两个连续整数的情况数,即可求出所求概率.
解答 解:列表如下:
| 1 | 2 | 3 | 4 | 5 | |
| 1 | --- | (2,1) | (3,1) | (4,1) | (5,1) |
| 2 | (1,2) | --- | (3,2) | (4,2) | (5,2) |
| 3 | (1,3) | (2,3) | --- | (4,3) | (5,3) |
| 4 | (1,4) | (2,4) | (3,4) | --- | (5,4) |
| 5 | (1,5) | (2,5) | (3,5) | (4,5) | --- |
则P(恰好是两个连续整数)=$\frac{8}{20}$=$\frac{2}{5}$,
故答案为:$\frac{2}{5}$
点评 此题考查了列表法与树状图法,概率=所求情况数与总情况数之比.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.正方形的正投影不可能是( )
| A. | 线段 | B. | 矩形 | C. | 正方形 | D. | 梯形 |
6.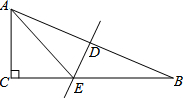 如图,在△ABC中,∠C=90°,∠B=22.5°,DE垂直平分AB,D为垂足,DE交BC于点E,若BE=15$\sqrt{2}$,则AC的长为( )
如图,在△ABC中,∠C=90°,∠B=22.5°,DE垂直平分AB,D为垂足,DE交BC于点E,若BE=15$\sqrt{2}$,则AC的长为( )
 如图,在△ABC中,∠C=90°,∠B=22.5°,DE垂直平分AB,D为垂足,DE交BC于点E,若BE=15$\sqrt{2}$,则AC的长为( )
如图,在△ABC中,∠C=90°,∠B=22.5°,DE垂直平分AB,D为垂足,DE交BC于点E,若BE=15$\sqrt{2}$,则AC的长为( )| A. | 15 | B. | 15$\sqrt{2}$ | C. | 30 | D. | 30$\sqrt{2}$ |
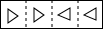
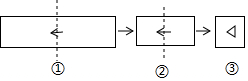 把一张长方形纸片按如图①、图②的方式从右向左连续对折两次后得到图③,再在图③中挖去一个如图所示的三角形小孔,则重新展开后得到的图形是( )
把一张长方形纸片按如图①、图②的方式从右向左连续对折两次后得到图③,再在图③中挖去一个如图所示的三角形小孔,则重新展开后得到的图形是( )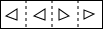

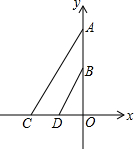 如图,平面直角坐标系中,A(0,10),B(0,5),点C是x轴上一点,点D为OC的中点.
如图,平面直角坐标系中,A(0,10),B(0,5),点C是x轴上一点,点D为OC的中点.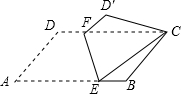 如图,将?ABCD沿EF对折,使点A落在点C处,若∠A=60°,AD=4,AB=6,则AE的长为$\frac{19}{4}$.
如图,将?ABCD沿EF对折,使点A落在点C处,若∠A=60°,AD=4,AB=6,则AE的长为$\frac{19}{4}$.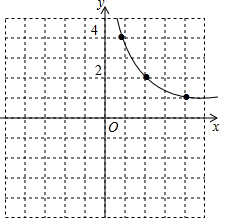 已知反比例函数y=$\frac{k}{x}$,图中已经画出了此函数图象的其中一支,请根据图中所给信息,把这个反比例函数图象的另一支补充完整.
已知反比例函数y=$\frac{k}{x}$,图中已经画出了此函数图象的其中一支,请根据图中所给信息,把这个反比例函数图象的另一支补充完整.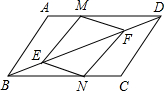 如图,在平行四边形ABCD中,点M、N 分别是AD、BC上的两点,点E、F在对角线BD上,且DM=BN,BE=DF.求证:四边形MENF是平行四边形.
如图,在平行四边形ABCD中,点M、N 分别是AD、BC上的两点,点E、F在对角线BD上,且DM=BN,BE=DF.求证:四边形MENF是平行四边形.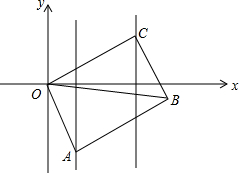 如图,已知?ABCD的顶点A、C分别在直线x=2和x=5上,O是坐标原点,则对角线OB长的最小值为7.
如图,已知?ABCD的顶点A、C分别在直线x=2和x=5上,O是坐标原点,则对角线OB长的最小值为7.