题目内容
构建一个图形,求出22.5°和67.5°的正切值.
考点:解直角三角形
专题:计算题
分析:在△ABC中,∠C=90°,AC=BC,延长CB到D,使BD=AB,连接AD,设AC=BC=x,根据等腰直角三角形的性质得∠ABC=45°,AB=
x,由于AB=BD=
x,则∠D=∠BAD,利用三角形外角性质可计算出∠D=22.5°,所以∠CAD=67.5°,然后在Rt△ADC中,根据正切的定义求解.
| 2 |
| 2 |
解答:解:如图, △ABC中,∠C=90°,AC=BC,延长CB到D,使BD=AB,连接AD,
△ABC中,∠C=90°,AC=BC,延长CB到D,使BD=AB,连接AD,
设AC=BC=x,
∵∠C=90°,AC=BC,
∴△ACB为等腰直角三角形,
∴∠ABC=45°,AB=
x,
∵BD=AB=
x,
∴∠D=∠BAD,
而∠ABC=∠D+∠BAD,
∴∠D=
×45°=22.5°,
∴∠CAD=67.5°,
在Rt△ADC中,tan∠D=
=
=
-1,
tan∠CAD=
=
=
+1,
即22.5°和67.5°的正切值分别为
-1,
+1.
 △ABC中,∠C=90°,AC=BC,延长CB到D,使BD=AB,连接AD,
△ABC中,∠C=90°,AC=BC,延长CB到D,使BD=AB,连接AD,设AC=BC=x,
∵∠C=90°,AC=BC,
∴△ACB为等腰直角三角形,
∴∠ABC=45°,AB=
| 2 |
∵BD=AB=
| 2 |
∴∠D=∠BAD,
而∠ABC=∠D+∠BAD,
∴∠D=
| 1 |
| 2 |
∴∠CAD=67.5°,
在Rt△ADC中,tan∠D=
| AC |
| CD |
| x | ||
|
| 2 |
tan∠CAD=
| CD |
| AC |
| ||
| x |
| 2 |
即22.5°和67.5°的正切值分别为
| 2 |
| 2 |
点评:本题考查了解直角三角形:在直角三角形中,由已知元素求未知元素的过程就是解直角三角形.充分利用特殊角的三角函数值解决问题.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
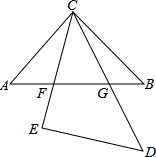 如图是两块等腰直角三角板放置在一起,AC=BC,∠ACB=90°,CE=DE,∠E=90°,CE交AB于F,CD交AB于G.求证:AF2+BG2=FG2.
如图是两块等腰直角三角板放置在一起,AC=BC,∠ACB=90°,CE=DE,∠E=90°,CE交AB于F,CD交AB于G.求证:AF2+BG2=FG2.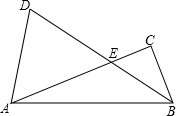 在Rt△ABC中,∠C=90°,∠CAB=α,边AB绕点B按顺时针方向旋转2α得到DB,交AC边点E,连接AD,当
在Rt△ABC中,∠C=90°,∠CAB=α,边AB绕点B按顺时针方向旋转2α得到DB,交AC边点E,连接AD,当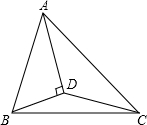 如图,已知S△ABC=8m2,AD平分∠BAC,且AD⊥BD于点D,则S△ADC=
如图,已知S△ABC=8m2,AD平分∠BAC,且AD⊥BD于点D,则S△ADC=