题目内容
已知△ABC的外接圆⊙O,过O引BC的垂线OH,试问∠COH与∠A之间有何关系?
考点:圆周角定理,垂径定理
专题:
分析:根据题意画出图形,根据垂径定理得出∠COH=
∠BOC,再由圆周角定理即可得出结论.
| 1 |
| 2 |
解答: 解:∠COH=∠A.
解:∠COH=∠A.
理由:如图所示,连接OB,OC,
∵OH⊥BC,
∴∠COH=
∠BOC.
∵∠BOC与∠A是同弧所对的圆心角与圆周角,
∴∠A=
∠BOC=∠COH.
 解:∠COH=∠A.
解:∠COH=∠A.理由:如图所示,连接OB,OC,
∵OH⊥BC,
∴∠COH=
| 1 |
| 2 |
∵∠BOC与∠A是同弧所对的圆心角与圆周角,
∴∠A=
| 1 |
| 2 |
点评:本题考查的是圆周角定理,熟知在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半是解答此题的关键.

练习册系列答案
相关题目
下列说法中,正确的是( )
| A、两腰对应相等的两个等腰三角形全等 |
| B、两角及其夹边对应相等的两个三角形全等 |
| C、两锐角对应相等的两个直角三角形全等 |
| D、面积相等的两个三角形全等 |
 如图所示,已知等腰直角三角形ABC的直角边长与正方形MNPQ的边长均为20cm,AC与MN在同一直线上,开始时点A与点N重合,让△ABC以每秒2cm的速度向左运动,最终点A与点M重合.
如图所示,已知等腰直角三角形ABC的直角边长与正方形MNPQ的边长均为20cm,AC与MN在同一直线上,开始时点A与点N重合,让△ABC以每秒2cm的速度向左运动,最终点A与点M重合. 从三角形木板上截下一块圆形的木板,
从三角形木板上截下一块圆形的木板,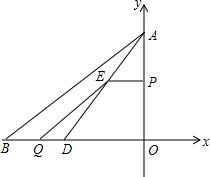 已知:如图,把Rt△ABC放在直角坐标系中,A(0,4)B(-5,0),点D在BC上,且CD=3,现有两个动点P,Q分别从点A和点B同时出发,其中点P以1个单位/秒的速度沿y轴负方向移动,点Q以
已知:如图,把Rt△ABC放在直角坐标系中,A(0,4)B(-5,0),点D在BC上,且CD=3,现有两个动点P,Q分别从点A和点B同时出发,其中点P以1个单位/秒的速度沿y轴负方向移动,点Q以