题目内容
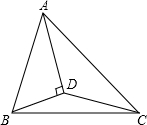 如图,已知S△ABC=8m2,AD平分∠BAC,且AD⊥BD于点D,则S△ADC=
如图,已知S△ABC=8m2,AD平分∠BAC,且AD⊥BD于点D,则S△ADC=考点:等腰三角形的判定与性质,三角形的面积
专题:
分析:延长BD交AC于点E,则可知△ABE为等腰三角形,则S△ABD=S△ADE,S△BDC=S△CDE,可得出S△ADC=
S△ABC.
| 1 |
| 2 |
解答:解:如图,延长BD交AC于点E,
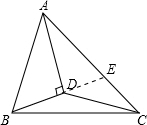
∵AD平分∠BAE,AD⊥BD,
∴∠BAD=∠EAD,∠ADB=∠ADE,
在△ABD和△AED中,
,
∴△ABD≌△AED(ASA),
∴BD=DE,
∴S△ABD=S△ADE,S△BDC=S△CDE,
∴S△ABD+S△BDC=S△ADE+S△CDE=S△ADC,
∴S△ADC═
S△ABC=
×8=4(m2),
故答案为:4.

∵AD平分∠BAE,AD⊥BD,
∴∠BAD=∠EAD,∠ADB=∠ADE,
在△ABD和△AED中,
|
∴△ABD≌△AED(ASA),
∴BD=DE,
∴S△ABD=S△ADE,S△BDC=S△CDE,
∴S△ABD+S△BDC=S△ADE+S△CDE=S△ADC,
∴S△ADC═
| 1 |
| 2 |
| 1 |
| 2 |
故答案为:4.
点评:本题主要考查等腰三角形的判定和性质,由BD=DE得到S△ABD=S△ADE,S△BDC=S△CDE是解题的关键.

练习册系列答案
相关题目
下列说法中,正确的是( )
| A、两腰对应相等的两个等腰三角形全等 |
| B、两角及其夹边对应相等的两个三角形全等 |
| C、两锐角对应相等的两个直角三角形全等 |
| D、面积相等的两个三角形全等 |
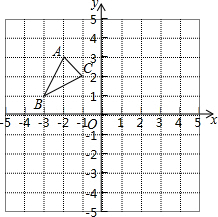 如图,△ABC三个顶点的坐标分别为A(-2,3),B(-3,1),C(-1,2).
如图,△ABC三个顶点的坐标分别为A(-2,3),B(-3,1),C(-1,2).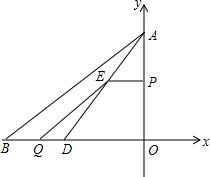 已知:如图,把Rt△ABC放在直角坐标系中,A(0,4)B(-5,0),点D在BC上,且CD=3,现有两个动点P,Q分别从点A和点B同时出发,其中点P以1个单位/秒的速度沿y轴负方向移动,点Q以
已知:如图,把Rt△ABC放在直角坐标系中,A(0,4)B(-5,0),点D在BC上,且CD=3,现有两个动点P,Q分别从点A和点B同时出发,其中点P以1个单位/秒的速度沿y轴负方向移动,点Q以