题目内容
7. 如图所示,△ABC中,∠B=30°,∠C=45°,AC=2,求AB和BC的长.
如图所示,△ABC中,∠B=30°,∠C=45°,AC=2,求AB和BC的长.
分析 根据锐角三角形函数和勾股定理可以求得AB和BC的长,本题得以解决.
解答  解:作AD⊥BC于点D,
解:作AD⊥BC于点D,
∵∠C=45°,AC=2,∠ADC=90°,
∴AD=CD=$\sqrt{2}$,
∵∠ADB=90°,∠B=30°,AD=$\sqrt{2}$,
∴AB=2$\sqrt{2}$,BD=$\sqrt{6}$,
∴BC=BD+CD=$\sqrt{6}+\sqrt{2}$,
即AB=$2\sqrt{2}$,BC=$\sqrt{6}+\sqrt{2}$.
点评 本题考查解直角三角形,解题的关键是明确题意,找出所求问题需要的条件.

练习册系列答案
相关题目
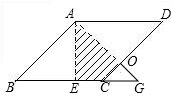 如图,在边长为2的菱形ABCD中,∠B=45°,AE为BC边上的高,将△ABE沿AE所在直线翻折后得△AGE,那么△AGE与四边形AECD重叠部分的面积是多少?
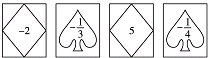
如图,在边长为2的菱形ABCD中,∠B=45°,AE为BC边上的高,将△ABE沿AE所在直线翻折后得△AGE,那么△AGE与四边形AECD重叠部分的面积是多少? 的卡片,那么加上卡片上的数字,如果抽到形如
的卡片,那么加上卡片上的数字,如果抽到形如 的卡片,那么减去卡片上的数字;
的卡片,那么减去卡片上的数字;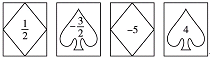
 如图,A、P、B、C是⊙O上的四个点,∠APC=∠CPB=60°.
如图,A、P、B、C是⊙O上的四个点,∠APC=∠CPB=60°.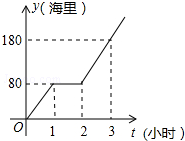 diaoyudao自古就是中国领土,中国政府已对钓鱼开展常态化巡逻.某人,为按计划准点到达指定海拔,某巡逻艇凌晨1:00出发,匀速行驶一段时间后,因中途出现故障耽搁了一段时间,故障排除后,该艇加快速度仍匀速前进,结果恰好准点到达.如图是该艇行驶的路程y(海里)与所用时间t(小时)的函数图象,求该巡逻艇原计划准点到的时间.
diaoyudao自古就是中国领土,中国政府已对钓鱼开展常态化巡逻.某人,为按计划准点到达指定海拔,某巡逻艇凌晨1:00出发,匀速行驶一段时间后,因中途出现故障耽搁了一段时间,故障排除后,该艇加快速度仍匀速前进,结果恰好准点到达.如图是该艇行驶的路程y(海里)与所用时间t(小时)的函数图象,求该巡逻艇原计划准点到的时间.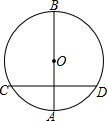 如图,AB是⊙O的直径,弦CD垂直平分OA,求劣弧CD所对的圆周角的度数.
如图,AB是⊙O的直径,弦CD垂直平分OA,求劣弧CD所对的圆周角的度数.