题目内容
5．
如图，点A、P、B、C是⊙O上的四点，且满足∠BAC=∠APC=60°，求证：△ABC是等边三角形．
分析 由∠BAC=∠APC=60°，根据圆周角定理，可求得△ABC的各内角的度数，继而证得△ABC是等边三角形．
解答 解：在△ABC中，
∵∠B=∠APC，且∠APC=60°，
∴∠B=60°，
又∵∠BAC=60°，
∴∠ACB=180°-∠BAC-∠ABC=180°-60°-60°=60°，
∴△ABC是等边三角形．
点评 此题考查了圆周角定理、等边三角形的判定与性质，熟练掌握圆周角定理是解题的关键．
练习册系列答案
相关题目
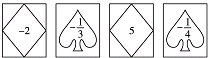
的卡片，那么加上卡片上的数字，如果抽到形如
的卡片，那么减去卡片上的数字；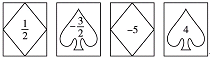
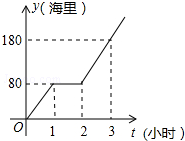diaoyudao自古就是中国领土，中国政府已对钓鱼开展常态化巡逻．某人，为按计划准点到达指定海拔，某巡逻艇凌晨1：00出发，匀速行驶一段时间后，因中途出现故障耽搁了一段时间，故障排除后，该艇加快速度仍匀速前进，结果恰好准点到达．如图是该艇行驶的路程y（海里）与所用时间t（小时）的函数图象，求该巡逻艇原计划准点到的时间．
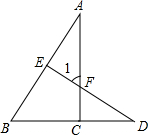如图所示，AC⊥BD于点C，DE⊥AB于点E．
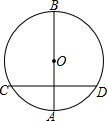如图，AB是⊙O的直径，弦CD垂直平分OA，求劣弧CD所对的圆周角的度数．
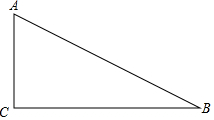如图Rt△ABC，作一个圆，使圆心O在AC上，且与AB、BC所在直线相切，并说明作图理由．