题目内容
6.对于整数a,b,c,d,规定符号$\left|\begin{array}{l}a&b\\ d&c\end{array}\right|$=ac-bd,已知$\left|\begin{array}{cc}1&b\\ d&6\end{array}\right|$的值大于2且小于4,则b+d的值为±4.分析 根据定义可得2<6-bd<4,求出bd的范围,根据b、d均为整数可得bd=3,分4种情况分别求解.
解答 解:根据题中的新定义得:2<6-bd<4,
由6-bd>2,得:bd<4,
由6-bd<4,得:bd>2,
则2<bd<4,
∵b、d均为整数,
∴bd=3,
则当b=-1时,d=-3,b+d=-4;
当b=1时,d=3,b+d=4,
当b=-3时,d=-1,b+d=-4;
当b=3时,d=1,b+d=4,
综上b+d=4或-4.
故答案为:±4.
点评 此题考查了有理数的混合运算,由新定义得出不等式组是根本,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
16.下列各式中,正确的是( )
| A. | 23=8 | B. | $\root{3}{-8}$=2 | C. | $\sqrt{-16}$=-4 | D. | $\root{3}{9}=3$ |
14.-27的立方根为( )
| A. | ±3 | B. | 3 | C. | -3 | D. | 没有立方根 |
18.据统计,清明小长假首日市区8个主要封闭式景区(瘦西湖、大明寺、个园、何园、茱萸湾、凤凰岛、汉陵苑、双博馆)共接待游客11.56万人次,同比增长10.48%,将数据11.56万用科学记数法表示为( )
| A. | 1.156×103 | B. | 0.1156×104 | C. | 1.156×105 | D. | 1.156×104 |
15.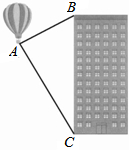 如图,热气球的探测器显示,从热气球A看一栋楼顶部B的仰角为30°,看这栋高楼底部C的俯角为60°,热气球A与高楼的水平距离为60m,这栋高楼BC的高度为( )
如图,热气球的探测器显示,从热气球A看一栋楼顶部B的仰角为30°,看这栋高楼底部C的俯角为60°,热气球A与高楼的水平距离为60m,这栋高楼BC的高度为( )
 如图,热气球的探测器显示,从热气球A看一栋楼顶部B的仰角为30°,看这栋高楼底部C的俯角为60°,热气球A与高楼的水平距离为60m,这栋高楼BC的高度为( )
如图,热气球的探测器显示,从热气球A看一栋楼顶部B的仰角为30°,看这栋高楼底部C的俯角为60°,热气球A与高楼的水平距离为60m,这栋高楼BC的高度为( )| A. | 80$\sqrt{3}$m | B. | 60$\sqrt{3}$m | C. | 40$\sqrt{3}$m | D. | 30$\sqrt{3}$m |
 阅读材料:
阅读材料: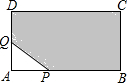 如图,长方形ABCD的边长分别为AB=12cm,AD=8cm,点P、Q都从点A出发,分别沿A-B,A-D运动,且保持AP=AQ=xcm,在这个变化过程中,图中的阴影部分的面积y(cm2)也随之变化.
如图,长方形ABCD的边长分别为AB=12cm,AD=8cm,点P、Q都从点A出发,分别沿A-B,A-D运动,且保持AP=AQ=xcm,在这个变化过程中,图中的阴影部分的面积y(cm2)也随之变化.