题目内容
17. 阅读材料:
阅读材料:关于三角函数还有如下的公式:
Sin(α±β)=sinαcosβ±cosαsinβ
tan(α±β)=$\frac{tanα±tanβ}{1μtanα•tanβ}$
利用这些公式可以将一些不是特殊角的三角函数转化为特殊角的三角函数来求值,
例:tan15°=tan(45°-30°)
=$\frac{tan45°-tan30°}{1+tan45°•tan30°}=\frac{{1-\frac{{\sqrt{3}}}{3}}}{{1+1×\frac{{\sqrt{3}}}{3}}}$
=$\frac{{(3-\sqrt{3})(3-\sqrt{3})}}{{(3+\sqrt{3})(3-\sqrt{3})}}$
=$\frac{{12-6\sqrt{3}}}{6}=2-\sqrt{3}$
根据以上阅读材料,请选择适当的公式解答下面的问题
(1)计算sin15°;
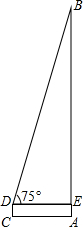
(2)我县体育场有一移动公司的信号塔,小明想利用所学的数学知识来测量该塔的高度,小华站在离塔底A距离7米的C处,测得塔顶的仰角为75°,小华的眼睛离地面的距离DC为1.62米,请帮助小华求出该信号塔的高度.(精确到0.1米,参考数据:$\sqrt{3}≈1.732,\sqrt{2}$≈1.414)
分析 (1)根据三角函数的公式,代入计算即可;
(2)根据仰角的概念、结合三角函数的公式、利用正切的定义计算.
解答 解:(1)
$\begin{array}{l}sin15°=sin(45°-30°)\\=sin45°cos30°-cos45°sin30°\\=\frac{{\sqrt{2}}}{2}•\frac{{\sqrt{3}}}{2}-\frac{{\sqrt{2}}}{2}•\frac{1}{2}\\=\frac{{\sqrt{6}-\sqrt{2}}}{4}\end{array}$
(2)在RT△BDE中,DE=AC=7,
∠BDE=75°,
tan∠BDE=$\frac{BE}{DE}$,
∴BE=DEtan∠BDE
=DEtan75°,
∵tan75°=tan(45°+30°)
$\begin{array}{l}=\frac{tan45°+tan30°}{1-tan45°tan30°}\\=\frac{{1+\frac{{\sqrt{3}}}{3}}}{{1-\frac{{\sqrt{3}}}{3}}}\\=\frac{{3+\sqrt{3}}}{{3-\sqrt{3}}}\\=2+\sqrt{3}\end{array}$
∴BE=7(2+$\sqrt{3}$)≈26.12,
∴信号塔AB的高度≈26.12+1.62≈27.7(米),
答:该信号塔AB的高度约为27.7米.
点评 本题考查的是解直角三角形的应用-仰角俯角问题,正确仰角俯角的概念、熟记锐角三角函数的定义、理解三角函数公式是解题的关键.

练习册系列答案
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案
相关题目
12.一个多边形的内角和是900°,则它是( )边形.
| A. | 八 | B. | 七 | C. | 六 | D. | 五 |
9.估算$\sqrt{28}$的值在( )
| A. | 7和8之间 | B. | 6和7之间 | C. | 5和6之间 | D. | 4和5之间 |
 如图,一架5米长的梯子AB,斜靠在一堵竖直的墙AO上,这时梯顶A距地面4米,若梯子沿墙下滑1米,则梯足B外滑1米.
如图,一架5米长的梯子AB,斜靠在一堵竖直的墙AO上,这时梯顶A距地面4米,若梯子沿墙下滑1米,则梯足B外滑1米. 如图,四边形ABCD是菱形,AB边上的高DE长为4cm,AE=3cm,动点P从点E出发,沿折线E-B-C向终点C运动,运动速度为1cm/s.动点Q从点B出发,沿折线B-C-D向终点D运动,运动速度为2cm/s,点P、Q同时出发,当其中的一个点到达终点时,另一点也随之停止运动,设点P的运动时间为t(s)
如图,四边形ABCD是菱形,AB边上的高DE长为4cm,AE=3cm,动点P从点E出发,沿折线E-B-C向终点C运动,运动速度为1cm/s.动点Q从点B出发,沿折线B-C-D向终点D运动,运动速度为2cm/s,点P、Q同时出发,当其中的一个点到达终点时,另一点也随之停止运动,设点P的运动时间为t(s)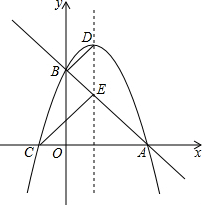 如图,直线y=-x+3与x轴交于A点,与y轴交于B点,对称轴为x=1的抛物线经过A、B两点,与x轴的另一个交点为C,抛物线与对称轴交于D点,连接CE、CB、BD.
如图,直线y=-x+3与x轴交于A点,与y轴交于B点,对称轴为x=1的抛物线经过A、B两点,与x轴的另一个交点为C,抛物线与对称轴交于D点,连接CE、CB、BD.