题目内容
7.计算:$\frac{1+2}{{1}^{2}-{2}^{2}}$+$\frac{2+3}{{2}^{2}-{3}^{2}}$+…$\frac{2013+2014}{201{3}^{2}-201{4}^{2}}$.分析 把分母利用平方差公式因式分解,约分得出-1-1-…-1(2013个-1),进一步计算得出答案即可.
解答 解:原式=$\frac{1+2}{(1-2)(1+2)}$+$\frac{2+3}{(2-3)(2+3)}$+…+$\frac{2013+2014}{(2013-2014)(2013+2014)}$
=-1-1-…-1
=-2013.
点评 此题考查因式分解的实际运用,掌握平方差公式是解决问题的关键.

练习册系列答案
 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
15.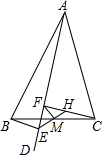 如图,△ABC中,AD是∠BAC内的一条射线,BE⊥AD,且△CHM可由△BEM旋转而得,则下列结论中错误的是( )
如图,△ABC中,AD是∠BAC内的一条射线,BE⊥AD,且△CHM可由△BEM旋转而得,则下列结论中错误的是( )
 如图,△ABC中,AD是∠BAC内的一条射线,BE⊥AD,且△CHM可由△BEM旋转而得,则下列结论中错误的是( )
如图,△ABC中,AD是∠BAC内的一条射线,BE⊥AD,且△CHM可由△BEM旋转而得,则下列结论中错误的是( )| A. | M是BC的中点 | B. | FM=$\frac{1}{2}$EH | C. | CF⊥AD | D. | FM⊥BC |
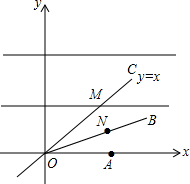 如图点A(2,0)点N在射线OB上运动,点M是直线y=x上一动点,OB为∠AOC的角平分线,求AN+MN的最小值,要画出图象.
如图点A(2,0)点N在射线OB上运动,点M是直线y=x上一动点,OB为∠AOC的角平分线,求AN+MN的最小值,要画出图象.