题目内容
15.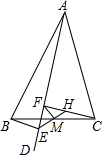 如图,△ABC中,AD是∠BAC内的一条射线,BE⊥AD,且△CHM可由△BEM旋转而得,则下列结论中错误的是( )
如图,△ABC中,AD是∠BAC内的一条射线,BE⊥AD,且△CHM可由△BEM旋转而得,则下列结论中错误的是( )| A. | M是BC的中点 | B. | FM=$\frac{1}{2}$EH | C. | CF⊥AD | D. | FM⊥BC |
分析 如图,由旋转变换的性质可知:△CHM≌△BEM,得到MH=ME,BM=CM,故选项A正确;容易证明CF∥BE,结合BE⊥AE,得到FH⊥AD,故选项C正确;由选项C知:△EFH为直角三角形,得到选项B正确.
解答  解:如图,∵△CHM可由△BEM旋转得到,
解:如图,∵△CHM可由△BEM旋转得到,
∴△CHM≌△BEM,
∴∠MCH=∠MBE,MH=ME,BM=CM,
∴选项A正确;
∵∠MCH=∠MBE,
∴CF∥BE,而BE⊥AE,
∴FH⊥AD,
∴FM为直角△EFH的斜边上的中线,
∴FM=$\frac{1}{2}$EH,
∴选项B、C正确;
故选D.
点评 该题主要考查了旋转变换的性质、平行线的判定、直角三角形的性质等知识点的应用问题;试题难度中等;牢固掌握旋转变换的性质、平行线的判定、直角三角形的性质等知识点是解题的关键.

练习册系列答案
相关题目
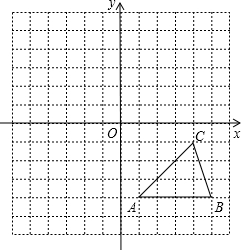 如图所示,方格纸中的每个小方格都是边长为1个单位长度的正方形,△ABC的顶点均在格点上,在建立平面直角坐标系后,点C的坐标为(4,-1).
如图所示,方格纸中的每个小方格都是边长为1个单位长度的正方形,△ABC的顶点均在格点上,在建立平面直角坐标系后,点C的坐标为(4,-1).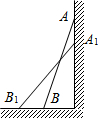 如图,一架2.5米长的梯子AB斜靠在竖直的墙AC上,这时B到墙C的距离为0.7米.
如图,一架2.5米长的梯子AB斜靠在竖直的墙AC上,这时B到墙C的距离为0.7米.