题目内容
3.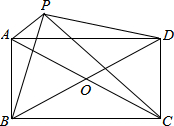 如图,?ABCD中,对角线AC、BD相交于点O,点P是四边形外一点,且PA⊥PC,PB⊥PD,垂足为P,且PA2+PC2=PB2+PD2.求证:四边形ABCD为矩形.
如图,?ABCD中,对角线AC、BD相交于点O,点P是四边形外一点,且PA⊥PC,PB⊥PD,垂足为P,且PA2+PC2=PB2+PD2.求证:四边形ABCD为矩形.
分析 由勾股定理得到AC=DB,然后再根据对角线相等的平行四边形是矩形可得结论.
解答 证明:∵PA⊥PC,PB⊥PD,
∴△APC和△BPD都是直角三角形,且∠APC=∠BPD=90°,
又PA2+PC2=PB2+PD2.
∴AC=BD,
又∵四边形ABCD是平行四边形,
∴平行四边形ABCD是矩形.
点评 此题主要考查了矩形的判定,以及勾股定理,关键是掌握对角线相等的平行四边形是矩形.

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
18.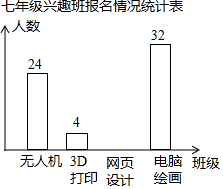 学校计划在七年级学生中开设4个信息技术应用兴趣班,分别为“无人机”班,“3D打印”班,“网页打印”班,“电脑绘画”班,规定每人最多参加一个班,自愿报名,根据报名的情况绘制了下面统计图,请回答问题.
学校计划在七年级学生中开设4个信息技术应用兴趣班,分别为“无人机”班,“3D打印”班,“网页打印”班,“电脑绘画”班,规定每人最多参加一个班,自愿报名,根据报名的情况绘制了下面统计图,请回答问题.
(1)报名参加兴趣班得到人数80人;统计表中的a=0.3,b=0.05;
(2)直接将统计图补充完整;
(3)为了均衡班级人数,在“电脑绘画”班中至少动员几人到“3D打印”班,才能使“电脑绘画”班人数不超过“3D打印”班人数的2倍.
七年级兴趣班报名情况统计表
 学校计划在七年级学生中开设4个信息技术应用兴趣班,分别为“无人机”班,“3D打印”班,“网页打印”班,“电脑绘画”班,规定每人最多参加一个班,自愿报名,根据报名的情况绘制了下面统计图,请回答问题.
学校计划在七年级学生中开设4个信息技术应用兴趣班,分别为“无人机”班,“3D打印”班,“网页打印”班,“电脑绘画”班,规定每人最多参加一个班,自愿报名,根据报名的情况绘制了下面统计图,请回答问题.(1)报名参加兴趣班得到人数80人;统计表中的a=0.3,b=0.05;
(2)直接将统计图补充完整;
(3)为了均衡班级人数,在“电脑绘画”班中至少动员几人到“3D打印”班,才能使“电脑绘画”班人数不超过“3D打印”班人数的2倍.
七年级兴趣班报名情况统计表
| 兴趣班名称 | 频率 |
| “无人机” | a |
| “3D打印” | b |
| “网页设计” | 0.25 |
| “电脑绘画” | 0.4 |
| 合计 | 1 |
8.下列运算正确的是( )
| A. | a3•a3=2a3 | B. | (a2)3=a6 | C. | 2x+3y=5xy | D. | 2-3=-6 |
15.一家游泳馆的游泳收费标准为25元/次,若购买会员年卡,可享受如下优惠:
例如,购买A类会员卡,一年内游泳20次,消费50+20×20=450元,若一年内在该游泳馆消费500元,则游泳次数最多的办卡方式是( )
| 会员年卡类型 | 办卡费用(元) | 每次游泳收费(元) |
| A类 | 50 | 20 |
| B类 | 150 | 15 |
| C类 | 300 | 10 |
| A. | 购买A类会员年卡 | B. | 购买B类会员年卡 | C. | 购买C类会员年卡 | D. | 不购买会员年卡 |
12.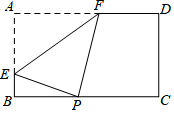 如图,矩形纸片ABCD中,AB=6,AD=10,P是边BC上的动点,现将纸片折叠,使点A与点P重合,折痕与矩形边的交点分别是E,F,要使折痕始终与边AB,AD有交点,则BP的取值范围是( )
如图,矩形纸片ABCD中,AB=6,AD=10,P是边BC上的动点,现将纸片折叠,使点A与点P重合,折痕与矩形边的交点分别是E,F,要使折痕始终与边AB,AD有交点,则BP的取值范围是( )
 如图,矩形纸片ABCD中,AB=6,AD=10,P是边BC上的动点,现将纸片折叠,使点A与点P重合,折痕与矩形边的交点分别是E,F,要使折痕始终与边AB,AD有交点,则BP的取值范围是( )
如图,矩形纸片ABCD中,AB=6,AD=10,P是边BC上的动点,现将纸片折叠,使点A与点P重合,折痕与矩形边的交点分别是E,F,要使折痕始终与边AB,AD有交点,则BP的取值范围是( )| A. | $\sqrt{5}≤BP≤5$ | B. | 2≤BP≤6 | C. | $\sqrt{5}≤BP≤6$ | D. | $2≤BP≤5\sqrt{3}$ |
7. 如图,△ABC是⊙O的内接三角形,连接OB、OC.若∠BOC=120°,则∠BAC的度数为( )
如图,△ABC是⊙O的内接三角形,连接OB、OC.若∠BOC=120°,则∠BAC的度数为( )
 如图,△ABC是⊙O的内接三角形,连接OB、OC.若∠BOC=120°,则∠BAC的度数为( )
如图,△ABC是⊙O的内接三角形,连接OB、OC.若∠BOC=120°,则∠BAC的度数为( )| A. | 30° | B. | 45° | C. | 60° | D. | 120° |
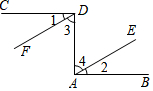 如图,已知CD⊥DA,DA⊥AB,∠1=∠2.试说明DF∥AE.请你完成下列填空,把证明过程补充完整.
如图,已知CD⊥DA,DA⊥AB,∠1=∠2.试说明DF∥AE.请你完成下列填空,把证明过程补充完整. 如图,在菱形ABCD中,AB=5,BD=8,点P,Q分别在BD,AD上,则AP+PQ的最小值为$\frac{24}{5}$.
如图,在菱形ABCD中,AB=5,BD=8,点P,Q分别在BD,AD上,则AP+PQ的最小值为$\frac{24}{5}$.