题目内容
8.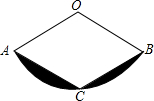 如图,扇形AOB中,OA=2,C为$\widehat{AB}$上的一点,连接AC,BC,如果四边形AOBC为菱形,则图中阴影部分的面积为( )
如图,扇形AOB中,OA=2,C为$\widehat{AB}$上的一点,连接AC,BC,如果四边形AOBC为菱形,则图中阴影部分的面积为( )| A. | $\frac{2π}{3}$-$\sqrt{3}$ | B. | $\frac{2π}{3}$-2$\sqrt{3}$ | C. | $\frac{4π}{3}$-$\sqrt{3}$ | D. | $\frac{4π}{3}$-2$\sqrt{3}$ |
分析 连接OC,过点A作AD⊥CD于点D,四边形AOBC是菱形可知OA=AC=2,再由OA=OC可知△AOC是等边三角形,∠AOC=∠BOC=60°,故△ACO与△BOC为边长相等的两个等边三角形,再根据锐角三角函数的定义得出AD的长,由S阴影=S扇形AOB-2S△AOC即可得出结论
解答 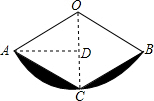 解:连接OC,过点A作AD⊥CD于点D,
解:连接OC,过点A作AD⊥CD于点D,
∵四边形AOBC是菱形,
∴OA=AC=2.
∵OA=OC,
∴△AOC是等边三角形,
∴∠AOC=∠BOC=60°
∴△ACO与△BOC为边长相等的两个等边三角形.
∵AO=2,
∴AD=OA•sin60°=2×$\frac{\sqrt{3}}{2}$=$\sqrt{3}$.
∴S阴影=S扇形AOB-2S△AOC=$\frac{120π×{2}^{2}}{360}$-2×$\frac{1}{2}$×2×$\sqrt{3}$=$\frac{4π}{3}$-2$\sqrt{3}$.
故选D.
点评 本题考查的是扇形面积的计算,熟记扇形的面积公式及菱形的性质是解答此题的关键.

练习册系列答案
相关题目
16.在一次社会调查活动中,小明调查了一个路口的车流量,具体数据如下:
在这组数据中,众数和中位数依次是( )
| 时间段 | 7~8点 | 8~9点 | 9~10点 | 10~11点 | 11~12点 |
| 数量/辆 | 68 | 56 | 50 | 68 | 54 |
| A. | 56,68 | B. | 68,56 | C. | 68,55 | D. | 68,50 |
13.$\frac{1}{4}$的倒数是( )
| A. | -$\frac{1}{4}$ | B. | -4 | C. | $\frac{1}{4}$ | D. | 4 |
17.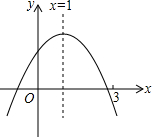 二次函数y=ax2+bx+c(a≠0)图象如图所示.下列结论中,错误的是( )
二次函数y=ax2+bx+c(a≠0)图象如图所示.下列结论中,错误的是( )
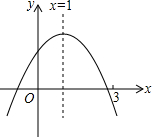 二次函数y=ax2+bx+c(a≠0)图象如图所示.下列结论中,错误的是( )
二次函数y=ax2+bx+c(a≠0)图象如图所示.下列结论中,错误的是( )| A. | abc<0 | |
| B. | 当m≠1时,a+b>am2+bm | |
| C. | 2a+b=0 | |
| D. | 若ax12+bx1=ax22+bx2且x1≠x2,x1+x2=3 |
18.已知三角形三条边的长度是三个连续的自然数,且它的周长小于18,符合上述条件的三角形有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |