题目内容
7.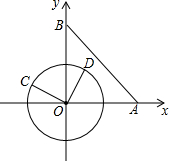 在平面直角坐标系xOy中,已知点A(6,0)、点B(0,6),动点C在以半径为3的⊙O上,连接OC,过O点作OD⊥OC,OD与⊙O相交于点D(其中点C、O、D按逆时针方向排列)连接AB
在平面直角坐标系xOy中,已知点A(6,0)、点B(0,6),动点C在以半径为3的⊙O上,连接OC,过O点作OD⊥OC,OD与⊙O相交于点D(其中点C、O、D按逆时针方向排列)连接AB(1)当OC∥AB时,∠BOC的度数为45°或135°
(2)判断AB与⊙O的位置关系.并说明理由:
(3)连接BC、AD,当OC∥AD时,求证:直线BC为⊙O的切线.
分析 (1)根据点A和点B坐标易得△OAB为等腰直角三角形,则∠OBA=45°,由于OC∥AB,所以当C点在y轴左侧时,有∠BOC=∠OBA=45°;当C点在y轴右侧时,有∠BOC=180°-∠OBA=135°,从而得出答案;
(2)根据圆心O到AB的距离即可得到答案;
(3)由于OC=3,CF=$\frac{3}{2}$,得出∠COF=30°,则可得到BOC=60°,∠AOD=60°,然后根据“SAS”判断△BOC≌△AOD,从而得出∠BCO=∠ADO=90°,再根据切线的判定定理可确定直线BC为⊙O的切线.
解答 解:(1)∵点A(6,0),点B(0,6),
∴OA=OB=6,
∴△OAB为等腰直角三角形,
∴∠OBA=45°,
∵OC∥AB,
∴当C点在y轴左侧时,∠BOC=∠OBA=45°;
当C点在y轴右侧时,∠BOC=90°+∠OBA=135°;
综上所述:当OC∥AB时,∠BOC的度数为45°或135°,
故答案为:45°或135°.
(2)AB与⊙O相离,理由:
∵由(1)证得△OAB为等腰直角三角形,
∴点O到AB的距离=$\frac{1}{2}$AB=$\frac{1}{2}$$\sqrt{O{A}^{2}+O{B}^{2}}$=3$\sqrt{2}$>3,
∴AB与⊙O相离;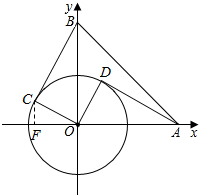
(3)直线BC为为⊙O的切线,理由如下:
如图:在Rt△OCF中,OC=3,CF=$\frac{3}{2}$,
∴sin∠COF=$\frac{CF}{OC}$=$\frac{1}{2}$,
∴∠COF=30°,
∴∠OAD=30°,
∴∠BOC=60°,∠AOD=60°,
在△BOC和△AOD中,
$\left\{\begin{array}{l}{OC=OD}\\{∠BOC=∠AOD}\\{BO=AO}\end{array}\right.$,
∴△BOC≌△AOD(SAS),
∴∠BCO=∠ADO=90°,
∴OC⊥BC,
∴直线BC是⊙O的切线;
点评 本题考查了圆的综合题,用到的知识点是切线的判定定理、平行线的性质和等腰直角三角形的判定与性质;熟练运用勾股定理和相似比进行几何计算是本题的关键.

 核心素养学练评系列答案
核心素养学练评系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案| 补贴数额(元) | 10 | 20 | … |
| 种植亩数(亩) | 160 | 240 | … |
(1)分别求出政府补贴政策实施后,种植亩数y(亩).每亩花木的收益z(元)与政府补贴数额x(元)之间的函数关系式;
(2)要使全县新种植的花木总收益W(元)最大,又要从政府的角度出发,政府应将每亩补贴数额x定为多少元?并求出总收益W的最大值和此时种植亩数;(总收益=每亩收益×亩数)
(3)在(2)问中取得最大总收益的情况下,需占用其中不超过50亩的新种花木园,利用其树间空地种植新品种花木,已知引进该新品种平均每亩的费用为530元,此外还要购置其他设备,这一费用(元)等于种植面积(亩)的平方的25倍.这样混种了新品种花木的这部分土地比原来种植单一品种花木时每亩的平均收益增加了2000元,这部分混种土地在扣除所有费用后总收益为80000元,求混种花木的土地有多少亩?
| 时间段 | 7~8点 | 8~9点 | 9~10点 | 10~11点 | 11~12点 |
| 数量/辆 | 68 | 56 | 50 | 68 | 54 |
| A. | 56,68 | B. | 68,56 | C. | 68,55 | D. | 68,50 |
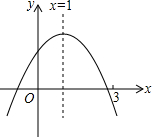 二次函数y=ax2+bx+c(a≠0)图象如图所示.下列结论中,错误的是( )
二次函数y=ax2+bx+c(a≠0)图象如图所示.下列结论中,错误的是( )| A. | abc<0 | |
| B. | 当m≠1时,a+b>am2+bm | |
| C. | 2a+b=0 | |
| D. | 若ax12+bx1=ax22+bx2且x1≠x2,x1+x2=3 |