题目内容
在△ABC中，∠A、∠B、∠C的对边分别是a、b、c，且满足∠A：∠B：∠C=1：2：3，则△ABC一定是（ ）
| A、直角三角形 | B、锐角三角形 |
| C、钝角三角形 | D、不能确定 |
考点：三角形内角和定理
专题：
分析：由∠A：∠B：∠C=1：2：3，设∠A、∠B、∠C的度数分别为x、2x、3x，根据三角形的内角和为180°列方程解答即可．
解答：解：设∠A、∠B、∠C的度数分别为x、2x、3x，由题意得
x+2x+3x=180
解得x=30
则2x=60，3x=90
∠C=90°
则△ABC一定是直角三角形．
故选：A．
x+2x+3x=180
解得x=30
则2x=60，3x=90
∠C=90°
则△ABC一定是直角三角形．
故选：A．
点评：此题考查三角形的内角和定理，利用三角之间的关系列方程解决问题是关键．
练习册系列答案
小学教材完全解读系列答案
相关题目
已知
与
都是关于x、y的方程y=kx+b的解，则k与b的值分别为（ ）
|
|
| A、k=-2，b=8 |
| B、k=-2，b=0 |
| C、k=2，b=8 |
| D、k=2，b=-8 |
如图，如果张力的位置可表示为（1，3），则王红的位置应表示为（ ）| A、（4，1） |
| B、（4，2） |
| C、（2，4） |
| D、（3，4） |
如图，将一条长为60cm的卷尺铺平后折叠，使得卷尺自身的一部分重合，然后在重合部分（阴影处）沿与卷尺边垂直的方向剪一刀，此时卷尺分为了三段，若这三段长度由短到长的比为1：2：3，则折痕对应的刻度的可能性有（ ）
| A、2种 | B、3种 | C、4种 | D、5种 |
在Rt△ABC中，∠C=90°，AB=10cm，AC=6cm，则BC的长为（ ）
| A、8cm | B、7cm |
| C、6cm | D、5cm |
已知正六边形的面积为6
，则其边长为（ ）
| 3 |
| A、2 | ||
| B、3 | ||
C、
| ||
D、2
|
若9a2+6（k-3）a+1是完全平方式，则k的值是（ ）
| A、±4 | B、±2 | C、3 | D、4或2 |
已知?ABCD中，AE平分∠BAD，CF平分∠BCD，分别交CD、AB于E、F，求证：AE=CF．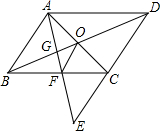
点E为平行四边形ABCD中DC边的延长线上的一点，且CE=DC，连接AE分别交BC、BD于点F、G，连接AC交BD于点O，连接OF．