题目内容
11. 如图,已知矩形ABCD的一条边AD=8cm,点P在CD边上,AP=AB,PC=4cm,连结PB.点M从点P出发,沿PA方向匀速运动(点M与点P、A不重合);点N同时从点B出发,沿线段AB的延长线匀速运动,连结MN交PB于点F.
如图,已知矩形ABCD的一条边AD=8cm,点P在CD边上,AP=AB,PC=4cm,连结PB.点M从点P出发,沿PA方向匀速运动(点M与点P、A不重合);点N同时从点B出发,沿线段AB的延长线匀速运动,连结MN交PB于点F.(1)求AB的长;
(2)若点M的运动速度为1cm/s,点N的运动速度为2cm/s,△AMN的面积为S,点M和点N的运动时间为t,求S与t的函数关系式,并求S的最大值;
(3)若点M和点N的运动速度相等,作ME⊥BP于点E.试问当点M、N在运动过程中,线段EF的长度是否发生变化?若变化,说明理由;若不变,求出线段EF的长度.
分析 (1)设AB=x,则AP=x,DP=x-4,在Rt△ADP中,由勾股定理得出方程,解方程即可;
(2)过M作MG⊥AN于G,则∠AGM=∠D=90°,证明△APD∽△MAG,得出对应边成比例求出MG=8-$\frac{4}{5}$t,由三角形面积即可得出S与t的关系式,再由二次函数的最值即可得出答案;
(3)作MQ∥AN,交PB于点Q,求出MP=MQ,BN=QM,得出MP=MQ,根据ME⊥PQ,得出EQ=$\frac{1}{2}$PQ,根据∠QMF=∠BNF,证出△MFQ≌△NFB,得出QF=$\frac{1}{2}$QB,再求出EF=$\frac{1}{2}$PB,由勾股定理求出PB,即可得出答案.
解答 解:(1)∵四边形ABCD是矩形,
∴AB∥CD,AB=CD,∠D=90°,
设AB=x,则AP=x,DP=x-4,
在Rt△ADP中,由勾股定理得:82+(x-4)2=x2,
解得:x=10,
∴AB=10;
(2)过M作MG⊥AN于G,则∠AGM=∠D=90°,
∵AB∥CD,
∴∠APD=∠MAG,
∴△APD∽△MAG,
∴$\frac{MG}{AD}=\frac{AM}{PA}$,即$\frac{MG}{8}=\frac{10-t}{10}$,
解得:MG=8-$\frac{4}{5}$t,
∵AN=10+2t,
∴S=$\frac{1}{2}$AN•MG=$\frac{1}{2}$(10+2t)(8-$\frac{4}{5}$t)=-$\frac{4}{5}$(t-$\frac{5}{2}$)2+45,
∴t=$\frac{5}{2}$时,S取得最大值为45;
(3)线段EF的长度不发生变化;理由如下:
作MQ∥AN,交PB于点Q,如图2,
∵AP=AB,MQ∥AN
∴∠APB=∠ABP=∠MQP.
∴MP=MQ,
∵BN=PM,
∴BN=QM.
∵MP=MQ,ME⊥PQ,
∴EQ=$\frac{1}{2}$PQ.
∵MQ∥AN,
∴∠QMF=∠BNF,
在△MFQ和△NFB中,$\left\{\begin{array}{l}{∠QFM=∠NFB}&{\;}\\{∠QMF=∠BNF}&{\;}\\{MQ=BN}&{\;}\end{array}\right.$,
∴△MFQ≌△NFB(AAS).
∴QF=$\frac{1}{2}$QB,
∴EF=EQ+QF=$\frac{1}{2}$PQ+$\frac{1}{2}$QB=$\frac{1}{2}$PB,
由(1)中的结论可得:PC=4,BC=8,∠C=90°,
∴PB=$\sqrt{{8}^{2}+{4}^{2}}$=4$\sqrt{5}$,
∴EF=$\frac{1}{2}$PB=2$\sqrt{5}$,
∴点M、N在移动过程中,线段EF的长度不变,它的长度为2$\sqrt{5}$.
点评 此题是四边形综合题目,考查了矩形的性质、相似三角形的判定与性质、全等三角形的判定与性质、勾股定理、等腰三角形的性质、二次函数的最值等知识;本题综合性强,有一定难度.

 名校课堂系列答案
名校课堂系列答案 某中学九年级1班同学积极响应“阳光体育工程”的号召,利用课外活动时间积极参加体育锻炼,每位同学从长跑、篮球、铅球、立定跳远中选一项进行训练,训练前后都进行了测试.现将项目选择情况及训练后篮球定时定点投篮测试成绩整理后作出如下统计图表.
某中学九年级1班同学积极响应“阳光体育工程”的号召,利用课外活动时间积极参加体育锻炼,每位同学从长跑、篮球、铅球、立定跳远中选一项进行训练,训练前后都进行了测试.现将项目选择情况及训练后篮球定时定点投篮测试成绩整理后作出如下统计图表.| 进球数(个) | 8 | 7 | 6 | 5 | 4 | 3 |
| 人数 | 2 | 1 | 4 | 7 | 8 | 2 |
请你根据图表中的信息回答下列问题:
(1)选择长跑训练的人数占全班人数的百分比为10%,该班学生的总人数为40;
(2)训练后篮球定时定点投篮人均进球数为5;
(3)若将选择篮球的同学的进球数写在外观、大小一样的枝条上,放在不透明的盒子中,搅拌均匀后,从中抽取一张,则抽到4的概率是多少?
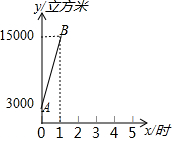 为节约能源,某市众多车主响应号召,将燃油汽车改装为天然气汽车.某日上午7:00-8:00,燃气公司给该市城西加气站的储气罐加气,8:00 加气站开始为前来的车辆加气.储气罐内的天然气总量y(立方米)随加气时间x(时)的变化而变化.
为节约能源,某市众多车主响应号召,将燃油汽车改装为天然气汽车.某日上午7:00-8:00,燃气公司给该市城西加气站的储气罐加气,8:00 加气站开始为前来的车辆加气.储气罐内的天然气总量y(立方米)随加气时间x(时)的变化而变化.| 时刻 | 8:00 | 9:00 | 10:00 | 11:00 | 12:00 |
| y(立方米) | 15000 | 7500 | 5000 | 3750 | 3000 |
(2)在8:00-12:00 范围内,y的变化情况如下表所示,请写出一个符合表格中数据的y关于x的函数解析式,依此函数解析式,判断上午9:05到9:20能否完成加气950立方米的任务,并说明理由.
| 温度/℃ | -8 | -1 | 7 | 15 | 21 | 24 | 30 |
| 天数 | 3 | 5 | 5 | 7 | 6 | 2 | 2 |
(1)该组数据的中位数是什么?
(2)若气温在18℃~25℃为市场“满意温度”,则该市一年中达到市民“满意温度”的大约有多少天?
 将如图所示的三棱柱展开,可以得到的图形是( )
将如图所示的三棱柱展开,可以得到的图形是( )| A. |  | B. |  | C. |  | D. |  |
 如图,某学校为了加固一篮球架,在下面焊接了一根钢筋撑杆AC,它与水平的钢板箱体成60°的夹角,且AB=0.5m.原有的上撑杆DE=1.6m,且∠BDE=135°.
如图,某学校为了加固一篮球架,在下面焊接了一根钢筋撑杆AC,它与水平的钢板箱体成60°的夹角,且AB=0.5m.原有的上撑杆DE=1.6m,且∠BDE=135°. 运动会上,甲、乙、丙三位同学进行跳绳比赛,通过“手心手背”游戏决定谁先跳,规则如下:三个人同时各用一只手随机出示手心或手背,若其中有一个人的手势与另外两个不同,则此人先进行比赛,若三个人手势相同,则重新决定,那么通过一次“手心手背”游戏,甲同学先跳绳的概率是多少?
运动会上,甲、乙、丙三位同学进行跳绳比赛,通过“手心手背”游戏决定谁先跳,规则如下:三个人同时各用一只手随机出示手心或手背,若其中有一个人的手势与另外两个不同,则此人先进行比赛,若三个人手势相同,则重新决定,那么通过一次“手心手背”游戏,甲同学先跳绳的概率是多少?