题目内容
3. 如图,某学校为了加固一篮球架,在下面焊接了一根钢筋撑杆AC,它与水平的钢板箱体成60°的夹角,且AB=0.5m.原有的上撑杆DE=1.6m,且∠BDE=135°.
如图,某学校为了加固一篮球架,在下面焊接了一根钢筋撑杆AC,它与水平的钢板箱体成60°的夹角,且AB=0.5m.原有的上撑杆DE=1.6m,且∠BDE=135°.(1)求撑杆AC的长;
(2)若篮板是边长为1m的正方形,上撑杆端点E在其中心位置,球篮连接篮板处为F,且EF=$\frac{1}{4}$m,下面的钢板箱体厚度为0.3m,CD=1.8m,则点F距地面的高度约为多少米?(结果精确到0.1m,参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73.
分析 (1)通过解直角三角形ABC得到AC 的长度即可;
(2)如图,过点E作EG⊥BD,交BD的延长线于点G.构建等腰Rt△DEG,通过解该直角三角形不难求得DG的长度,结合图形解F距地面的高度.
解答 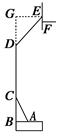 解:(1)在Rt△ABC中,$\frac{AB}{AC}$=cos60°,
解:(1)在Rt△ABC中,$\frac{AB}{AC}$=cos60°,
∴AC=$\frac{AB}{\frac{1}{2}}$=2AB=1m;
(2)在Rt△ABC中,BC=AB•tan60°=$\frac{\sqrt{3}}{2}$,
如图,过点E作EG⊥BD,交BD的延长线于点G.
在Rt△DEG中,∠EDG=180°-135°=45°,DE=1.6m,
∴DG=DE•cos45°=$\frac{4\sqrt{2}}{5}$m.
$\frac{4\sqrt{2}}{5}$-$\frac{1}{4}$+1.8+$\frac{\sqrt{3}}{2}$+0.3≈3.8(m).
答:F距地面的高度约为3.8m.
点评 本题考查了解直角三角形的应用.利用数学知识解决实际问题是中学数学的重要内容.解决此问题的关键在于正确理解题意的基础上建立数学模型,把实际问题转化为数学问题.

练习册系列答案
 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
18. 已知一次函数y=kx+b的图象如图所示,则不等式kx+b>-1的解集是( )
已知一次函数y=kx+b的图象如图所示,则不等式kx+b>-1的解集是( )
 已知一次函数y=kx+b的图象如图所示,则不等式kx+b>-1的解集是( )
已知一次函数y=kx+b的图象如图所示,则不等式kx+b>-1的解集是( )| A. | x>-2 | B. | x<-2 | C. | x>0 | D. | x<0 |
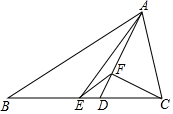 如图,△ABC中,AB=12,AC=5,AD是∠BAC角平分线,AE是BC边上的中线,过点C作CF⊥AD于F,连接EF,则线段EF的长为3.5.
如图,△ABC中,AB=12,AC=5,AD是∠BAC角平分线,AE是BC边上的中线,过点C作CF⊥AD于F,连接EF,则线段EF的长为3.5. 如图,已知矩形ABCD的一条边AD=8cm,点P在CD边上,AP=AB,PC=4cm,连结PB.点M从点P出发,沿PA方向匀速运动(点M与点P、A不重合);点N同时从点B出发,沿线段AB的延长线匀速运动,连结MN交PB于点F.
如图,已知矩形ABCD的一条边AD=8cm,点P在CD边上,AP=AB,PC=4cm,连结PB.点M从点P出发,沿PA方向匀速运动(点M与点P、A不重合);点N同时从点B出发,沿线段AB的延长线匀速运动,连结MN交PB于点F.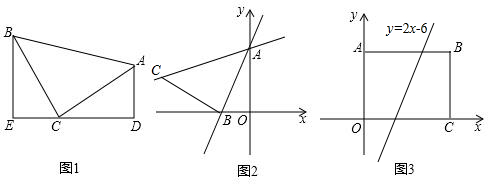
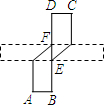 将一张长为70cm的长方形纸片ABCD沿对称轴EF折叠后得到如图所示的形状,若折叠后AB与CD的距离为60cm,则原纸片的宽度(AB)为10cm.
将一张长为70cm的长方形纸片ABCD沿对称轴EF折叠后得到如图所示的形状,若折叠后AB与CD的距离为60cm,则原纸片的宽度(AB)为10cm.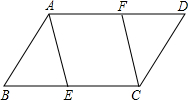 如图,已知四边形ABCD是平行四边形,若点E、F分别在边BC、AD上,连接AE、CF,若∠AEB=∠CFD.
如图,已知四边形ABCD是平行四边形,若点E、F分别在边BC、AD上,连接AE、CF,若∠AEB=∠CFD.