题目内容
6.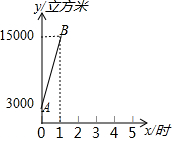 为节约能源,某市众多车主响应号召,将燃油汽车改装为天然气汽车.某日上午7:00-8:00,燃气公司给该市城西加气站的储气罐加气,8:00 加气站开始为前来的车辆加气.储气罐内的天然气总量y(立方米)随加气时间x(时)的变化而变化.
为节约能源,某市众多车主响应号召,将燃油汽车改装为天然气汽车.某日上午7:00-8:00,燃气公司给该市城西加气站的储气罐加气,8:00 加气站开始为前来的车辆加气.储气罐内的天然气总量y(立方米)随加气时间x(时)的变化而变化.| 时刻 | 8:00 | 9:00 | 10:00 | 11:00 | 12:00 |
| y(立方米) | 15000 | 7500 | 5000 | 3750 | 3000 |
(2)在8:00-12:00 范围内,y的变化情况如下表所示,请写出一个符合表格中数据的y关于x的函数解析式,依此函数解析式,判断上午9:05到9:20能否完成加气950立方米的任务,并说明理由.
分析 (1)根据点A、B的坐标,利用待定系数法即可求出直线AB的解析式,此题得解;
(2)根据表格数据可知在8:00-12:00 范围内,y与x之间满足反比例关系,结合表格中的数据可得出该函数解析式,再利用反比例函数图象上点的坐标特征求出9:05和9:20储气罐内的天然气的总量,做差比较后即可得出结论.
解答 解:(1)设直线AB的解析式为y=kx+b,
把点A(0,3000),B(1,15000)分别代入,
$\left\{\begin{array}{l}{b=3000}\\{k+b=15000}\end{array}\right.$,解得:$\left\{\begin{array}{l}{k=12000}\\{b=3000}\end{array}\right.$,
∴直线AB的解析式为y=12000x+3000.
答:在7:00-8:00 范围内,y关于x的函数解析式为y=12000x+3000.
(2)函数解析式为:y=$\frac{15000}{x}$(1≤x≤5).
验证如下:
当x=1时,y=15000,即上午8:00,x与y的值满足解析式.
同理,表格数据所对应的x与y的值都满足解析式.
当上午9:05即x=2$\frac{1}{12}$时,y=7200;
当上午9:20即x=2$\frac{1}{3}$时,y=$\frac{45000}{7}$.
∵7200-$\frac{45000}{7}$=$\frac{5400}{7}$,
又∵$\frac{5400}{7}$<950,
∴上午9:05到9:20不能完成加气950立方米的任务.
点评 本题考查了一次函数的应用、待定系数法求一次函数解析式以及反比例函数图象上点的坐标特征,解题的关键是:(1)根据点的坐标,利用待定系数法求出直线AB的解析式;(2)利用反比例函数图象上点的坐标特征求出9:05和9:20储气罐内的天然气的总量.

 阅读快车系列答案
阅读快车系列答案 已知一次函数y=kx+b的图象如图所示,则不等式kx+b>-1的解集是( )
已知一次函数y=kx+b的图象如图所示,则不等式kx+b>-1的解集是( )| A. | x>-2 | B. | x<-2 | C. | x>0 | D. | x<0 |
 如图是一个转盘,若转到红色则小明胜,转到黑色则小东胜,这个游戏对双方是否公平?请说明理由.
如图是一个转盘,若转到红色则小明胜,转到黑色则小东胜,这个游戏对双方是否公平?请说明理由.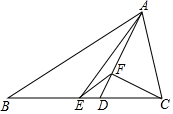 如图,△ABC中,AB=12,AC=5,AD是∠BAC角平分线,AE是BC边上的中线,过点C作CF⊥AD于F,连接EF,则线段EF的长为3.5.
如图,△ABC中,AB=12,AC=5,AD是∠BAC角平分线,AE是BC边上的中线,过点C作CF⊥AD于F,连接EF,则线段EF的长为3.5. 如图,已知矩形ABCD的一条边AD=8cm,点P在CD边上,AP=AB,PC=4cm,连结PB.点M从点P出发,沿PA方向匀速运动(点M与点P、A不重合);点N同时从点B出发,沿线段AB的延长线匀速运动,连结MN交PB于点F.
如图,已知矩形ABCD的一条边AD=8cm,点P在CD边上,AP=AB,PC=4cm,连结PB.点M从点P出发,沿PA方向匀速运动(点M与点P、A不重合);点N同时从点B出发,沿线段AB的延长线匀速运动,连结MN交PB于点F.