题目内容
等腰△ABC中,AB=AC=10,S△ABC=30,求底边BC.(分类讨论)
考点:勾股定理,等腰三角形的性质
专题:分类讨论
分析:首先利用三角形面积求法得出EC的长,再利用勾股定理得出AE以及BC的长.
解答: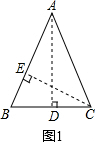 解:如图1,过点A作AD⊥BC于点D,过点C作CE⊥AB于点E,
解:如图1,过点A作AD⊥BC于点D,过点C作CE⊥AB于点E,
∵AB=AC=10,S△ABC=30,
∴
×EC×AB=30,
解得:EC=6,
∴AE=
=8,
∴BE=2,
∴BC=
=2
.
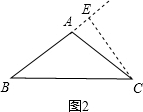 如图2,过点C作CE⊥AB于点E,
如图2,过点C作CE⊥AB于点E,
∵AB=AC=5,S△ABC=7.5,
∴
×EC×AB=30,
解得:EC=6,
∴AE=
=8,
∴BE=8+10=18,
∴BC=
=6
.
综上所述,BC的长是2
或6
.
 解:如图1,过点A作AD⊥BC于点D,过点C作CE⊥AB于点E,
解:如图1,过点A作AD⊥BC于点D,过点C作CE⊥AB于点E,∵AB=AC=10,S△ABC=30,
∴
| 1 |
| 2 |
解得:EC=6,
∴AE=
| AC2-EC2 |
∴BE=2,
∴BC=
| 22+62 |
| 10 |
 如图2,过点C作CE⊥AB于点E,
如图2,过点C作CE⊥AB于点E,∵AB=AC=5,S△ABC=7.5,
∴
| 1 |
| 2 |
解得:EC=6,
∴AE=
| AC2-EC2 |
∴BE=8+10=18,
∴BC=
| 182+62 |
| 10 |
综上所述,BC的长是2
| 10 |
| 10 |
点评:此题主要考查了勾股定理以及三角形面积,得出EC的长是解题关键.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
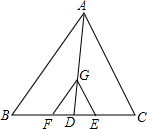 如图,在△ABC中,AD是中线,G是AD上一点,AG=2GD,CF∥AB,CE∥AC,分别交BC于点F、E.
如图,在△ABC中,AD是中线,G是AD上一点,AG=2GD,CF∥AB,CE∥AC,分别交BC于点F、E.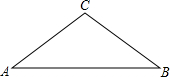 如图,△ABC中,BC=5,AC=5,AB=8.
如图,△ABC中,BC=5,AC=5,AB=8.
 如图,已知点D、F在△ABC的边AB上,点E在边AC上,且DE∥BC,
如图,已知点D、F在△ABC的边AB上,点E在边AC上,且DE∥BC,