题目内容
2.如图,在△ABC中,∠B=90°,AB=6cm,BC=12cm,动点P从A开始沿AB边向B以1cm/s的速度移动,动点Q从点B开始沿BC边向C以3cm/s的速度移动.已知P、Q分别从A、B同时出发,点P到B或点Q到C时,P与Q同时停止运动.
(1)求△PBQ的面积S(cm2)关于移动时间t(s)的函数关系式及t的取值范围.
(2)画出这个函数的图象.
(3)指出△PBQ的面积S随移动时间t如何变化.
分析 (1)根据题意可知:PB=6-t,BQ=3t,然后利用三角形的面积公式列出关系式即可;
(2)根据函数关系式画出图象即可;
(3)根据函数图象回答即可.
解答 解:(1)PB=AB-AP=6-t,BQ=3t.
S=$\frac{1}{2}$PB•BQ=$\frac{1}{2}×3t×(6-t)$=$-\frac{3}{2}{t}^{2}+9t$.
∴S与t的函数关系式为y=$-\frac{3}{2}{t}^{2}+9t$(0<t≤4)
(2)函数图象如图所示:
(3)根据函数图象可知:当0<t≤3时,S随t的增大而增大;当3≤t≤4时,S随t的增大而减小.
点评 本题主要考查的是动点问题的函数图象,根据三角形的面积公式列出函数关系式是解题的关键.

练习册系列答案
相关题目
13.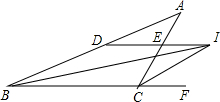 如图,△ABC中,BI,CI平分∠ABC,∠ACF,过点I作ID∥BC分别交AC,AB于点E,D.若BD=9cm,CE=4cm,则DE等于( )
如图,△ABC中,BI,CI平分∠ABC,∠ACF,过点I作ID∥BC分别交AC,AB于点E,D.若BD=9cm,CE=4cm,则DE等于( )
 如图,△ABC中,BI,CI平分∠ABC,∠ACF,过点I作ID∥BC分别交AC,AB于点E,D.若BD=9cm,CE=4cm,则DE等于( )
如图,△ABC中,BI,CI平分∠ABC,∠ACF,过点I作ID∥BC分别交AC,AB于点E,D.若BD=9cm,CE=4cm,则DE等于( )| A. | 2cm | B. | 5cm | C. | 4cm | D. | 5cm |
17.已知x=1是关于x的方程2x-a=0的解,则a的值是( )
| A. | -5 | B. | 5 | C. | 7 | D. | 2 |
14.一个多边形的每个外角都是45°,那么这个多边形的内角和等于( )
| A. | 720° | B. | 900° | C. | 675° | D. | 1080° |
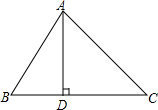 如图,在△ABC中,AD⊥BC,垂足为D,∠B=60°,∠C=45°.
如图,在△ABC中,AD⊥BC,垂足为D,∠B=60°,∠C=45°.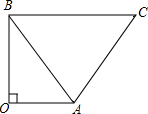 如图,在Rt△AOB中,∠O=90°,∠ABO=30°,以点A为旋转中心,把△ABO顺时针旋转得△ACD(D点未画出),当旋转后满足BC∥OA时,旋转角的大小为( )
如图,在Rt△AOB中,∠O=90°,∠ABO=30°,以点A为旋转中心,把△ABO顺时针旋转得△ACD(D点未画出),当旋转后满足BC∥OA时,旋转角的大小为( )