题目内容
19.用适当的方法解下列一元二次方程(1)4(x-1)2-36=0(直接开平方法)
(2)x2+2x-3=0(配方法)
(3)x(x-4)=8-2x(因式分解法)
(4)(x+1)(x-2)=4 (公式法)
分析 (1)方程整理后,利用直接开平方法求出解即可;
(2)方程整理后,利用配方法求出解即可;
(3)方程整理后,利用因式分解法求出解即可;
(4)方程整理为一般形式,找出a,b,c的值,代入求根公式即可求出解.
解答 解:(1)方程整理得:(x-1)2=9,
开方得:x-1=3或x-1=-3,
解得:x1=4,x2=-2;
(2)方程整理得:x2+2x=3,
配方得:x2+2x+1=4,即(x+1)2=4,
开方得:x+1=2或x+1=-2,
解得:x1=1,x2=-3;
(3)方程整理得:x(x-4)+2(x-4)=0,
分解因式得:(x-4)(x+2)=0,
解得:x1=4,x2=-2;
(4)方程整理得:x2-x-6=0,
这里a=1,b=-1,c=-6,
∵△=1+24=25,
∴x=$\frac{1±5}{2}$,
解得:x1=3,x2=-2.
点评 此题考查了解一元二次方程-因式分解法,熟练掌握因式分解的方法是解本题的关键.

练习册系列答案
 核心素养学练评系列答案
核心素养学练评系列答案
相关题目
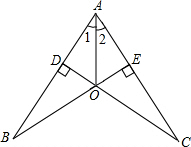 如图,CD⊥AB,BE⊥AC,垂足分别为D、E,BE、CD交于点O,OB=OC.求证:∠1=∠2.
如图,CD⊥AB,BE⊥AC,垂足分别为D、E,BE、CD交于点O,OB=OC.求证:∠1=∠2. (1)画出△ABC关于y轴对称的△A1B1C1;并写出△A1B1C1的各顶点的坐标.
(1)画出△ABC关于y轴对称的△A1B1C1;并写出△A1B1C1的各顶点的坐标. 如图,CD是⊙O的直径,∠EOD=72°,AE交⊙O于点B,且AB=OC,求∠A的度数.
如图,CD是⊙O的直径,∠EOD=72°,AE交⊙O于点B,且AB=OC,求∠A的度数.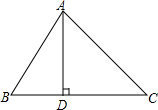 如图,在△ABC中,AD⊥BC,垂足为D,∠B=60°,∠C=45°.
如图,在△ABC中,AD⊥BC,垂足为D,∠B=60°,∠C=45°.