题目内容
如图，将△ABC沿它的中位线DE折叠后，点A落在点A′处，若∠A=20°，∠B=120°，则∠A′DC=考点：翻折变换（折叠问题）
专题：
分析：根据三角形内角和定理可得∠C的度数，根据三角形中位线的性质可得∠ADE的度数，根据折叠的性质可得∠A′DE的度数，再根据平角的定义即可求解．
解答：解：∵在△ABC中，∠A=20°，∠B=120°，
∴∠C=40°，
∵DE是△ABC的中位线，
∴∠ADE=∠C=40°，
由折叠的性质可知，∠A′DE=∠ADE=40°，
∴∠A′DC=180°-40°×2=100°．
故答案为：100．
∴∠C=40°，
∵DE是△ABC的中位线，
∴∠ADE=∠C=40°，
由折叠的性质可知，∠A′DE=∠ADE=40°，
∴∠A′DC=180°-40°×2=100°．
故答案为：100．
点评：本题考查了翻折变换的知识，解答本题的关键是根据翻折变换的性质：翻折前后对应角相等，得出∠ADE、∠ADE的度数相等，同时考查了三角形内角和定理和三角形中位线的性质．
练习册系列答案
第三学期赢在暑假系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案
相关题目
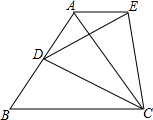如图，在等边△ABC的边AB上任意取一点D，作等边△CDE．
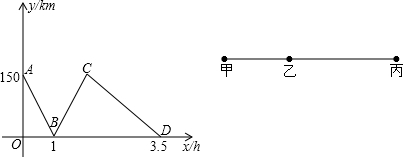两车同时出发同向而行，设慢车行驶的时间为x（h），两车之间的距离为y（km），图中的折线表示y与x之间的函数关系．根据图象进行以下探究：