题目内容
如图,甲丙两地相距500km,一列快车从甲地驶往丙地,且途中经过乙地;一列慢车从乙地驶往丙地,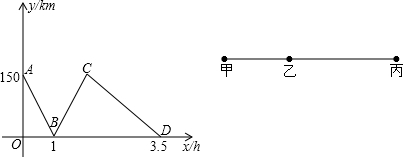 两车同时出发同向而行,设慢车行驶的时间为x(h),两车之间的距离为y(km),图中的折线表示y与x之间的函数关系.根据图象进行以下探究:
两车同时出发同向而行,设慢车行驶的时间为x(h),两车之间的距离为y(km),图中的折线表示y与x之间的函数关系.根据图象进行以下探究:
(1)甲乙两地之间的距离为 km;
(2)求慢车和快车的速度.
(3)求线段CD所表示的y与x之间的函数关系式,并写出自变量x的取值范围;
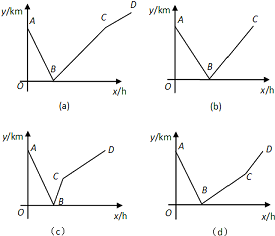
(4)若这列快车从甲地驶往丙地,慢车从丙地驶往甲地,两车同时出发相向而行,且两车的车速各自不变.设慢车行驶的时间为x(h),两车之间的距离为y(km),则下列四个图象中,哪一图象中的折线能表示此时y(千米)和时间x(小时)之间的函数关系,请写出你认为可能合理的代号,并直接写出折线中拐点A、B、C或A、B、C、D的坐标.
 两车同时出发同向而行,设慢车行驶的时间为x(h),两车之间的距离为y(km),图中的折线表示y与x之间的函数关系.根据图象进行以下探究:
两车同时出发同向而行,设慢车行驶的时间为x(h),两车之间的距离为y(km),图中的折线表示y与x之间的函数关系.根据图象进行以下探究:(1)甲乙两地之间的距离为
(2)求慢车和快车的速度.
(3)求线段CD所表示的y与x之间的函数关系式,并写出自变量x的取值范围;

(4)若这列快车从甲地驶往丙地,慢车从丙地驶往甲地,两车同时出发相向而行,且两车的车速各自不变.设慢车行驶的时间为x(h),两车之间的距离为y(km),则下列四个图象中,哪一图象中的折线能表示此时y(千米)和时间x(小时)之间的函数关系,请写出你认为可能合理的代号,并直接写出折线中拐点A、B、C或A、B、C、D的坐标.
考点:一次函数的应用
专题:压轴题
分析:(1)x=0时的y值即为甲、乙两地间的距离;
(2)先根据速度=路程÷时间求出慢车的速度,再设快车的速度是vkm/h,然后根据1小时时快车追上慢车列出方程求解即可;
(3)先求出C点的横坐标,即快车到达丙地的时间,再根据追击问题求出此时两车间的距离,从而得到点C的坐标,然后利用待定系数法求出线段CD的函数解析式即可;
(4)快车和慢车500÷(100+250)=
小时相遇;500÷250=2小时快车从甲地到达丙地;500÷100=5小时慢车从丙地到达甲地,依此即可求解.
(2)先根据速度=路程÷时间求出慢车的速度,再设快车的速度是vkm/h,然后根据1小时时快车追上慢车列出方程求解即可;
(3)先求出C点的横坐标,即快车到达丙地的时间,再根据追击问题求出此时两车间的距离,从而得到点C的坐标,然后利用待定系数法求出线段CD的函数解析式即可;
(4)快车和慢车500÷(100+250)=
| 10 |
| 7 |
解答:解:(1)∵点A(0,150),
∴甲乙两地之间的距离为150km;
(2)慢车速度:(500-150)÷3.5=100km/h;
快车速度:150+100=250km/h;
(3)500÷250=2h,
350-100×2=150km,
∴点C坐标为(2,150),
设yCD=kx+b,
把点C(2,150),D(3.5,0)代入得
,
解得
.
∴yCD=-100x+350(2≤x≤3.5).
(4)由分析可知,图象(c)中的折线能表示此时y(千米)和时间x(小时)之间的函数关系,A(0,500)、B(
,0)、C(2,150)、D(5,500).
∴甲乙两地之间的距离为150km;
(2)慢车速度:(500-150)÷3.5=100km/h;
快车速度:150+100=250km/h;
(3)500÷250=2h,
350-100×2=150km,
∴点C坐标为(2,150),
设yCD=kx+b,
把点C(2,150),D(3.5,0)代入得
|
解得
|
∴yCD=-100x+350(2≤x≤3.5).
(4)由分析可知,图象(c)中的折线能表示此时y(千米)和时间x(小时)之间的函数关系,A(0,500)、B(
| 10 |
| 7 |
点评:此题考查一次函数的综合运用,解答问题的关键是看清图象表示的意义,利用路程、时间、速度三者之间的关系解决问题.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
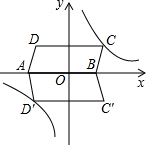 平行四边形ABCD在平面直角坐标系中的位置如图所示,其中A(-6,0),B(4,0),C(5,3),反比例函数y=
平行四边形ABCD在平面直角坐标系中的位置如图所示,其中A(-6,0),B(4,0),C(5,3),反比例函数y= 如图,点E、F分别是?ABCD的边BC、AD上的点,且CE=AF.
如图,点E、F分别是?ABCD的边BC、AD上的点,且CE=AF. 已知,直线y=-
已知,直线y=- 如图,将△ABC沿它的中位线DE折叠后,点A落在点A′处,若∠A=20°,∠B=120°,则∠A′DC=
如图,将△ABC沿它的中位线DE折叠后,点A落在点A′处,若∠A=20°,∠B=120°,则∠A′DC=