题目内容
10.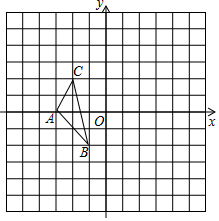 如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC(顶点是网格线的交点),已知△ABC三个顶点为A(-3,0)、B(-1,-2)、C(-2,2)和格点D(0,1).
如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC(顶点是网格线的交点),已知△ABC三个顶点为A(-3,0)、B(-1,-2)、C(-2,2)和格点D(0,1).(1)将△ABC向下平移4个单位,画出平移后得到的△A′B′C′;
(2)画出△ABC关于点D成中心对称的△A1B1C1;若点P(a,b)为△ABC内任意一点,请直接写出这次图形变换后,P的对应点P1的坐标(用a、b的代数式表示).
分析 (1)根据图形平移的性质画出平移后得到的△A′B′C′即可;
(2)画出△ABC关于点D成中心对称的△A1B1C1;,根据A点坐标的变化即可得出结论.
解答  解:(1)如图,△A′B′C′即为所求;
解:(1)如图,△A′B′C′即为所求;
(2)如图,△A1B1C1即为所求,
∵B(-1,-2),B1(1,4),
∴点P(a,b),则P1(-a,-b+2).
点评 本题考查的是作图-旋转变换,熟知图形旋转不变性的性质是解答此题的关键.

练习册系列答案
相关题目
1.下列运算正确的是( )
| A. | (-a3)2=a6 | B. | xp•yp=(xy)2p | C. | x6÷x3=x2 | D. | (m+n)2=m2+n2 |
5.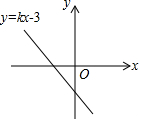 若函数y=kx-3的图象如图所示,则一元二次方程x2+x+k-1=0根的存在情况是( )
若函数y=kx-3的图象如图所示,则一元二次方程x2+x+k-1=0根的存在情况是( )
 若函数y=kx-3的图象如图所示,则一元二次方程x2+x+k-1=0根的存在情况是( )
若函数y=kx-3的图象如图所示,则一元二次方程x2+x+k-1=0根的存在情况是( )| A. | 有两个不相等的实数根 | B. | 有两个相等的实数根 | ||
| C. | 没有实数根 | D. | 无法确定 |
19.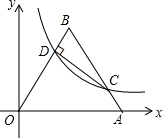 如图,将边长为2的等边△OAB放置于平面直角坐标系xOy中,C是AB边上的一个点(不与端点A、B重合),作CD⊥OB于点D,若点C、D都在双曲线y=$\frac{k}{x}$上(k>0,x>0),则k的值为( )
如图,将边长为2的等边△OAB放置于平面直角坐标系xOy中,C是AB边上的一个点(不与端点A、B重合),作CD⊥OB于点D,若点C、D都在双曲线y=$\frac{k}{x}$上(k>0,x>0),则k的值为( )
 如图,将边长为2的等边△OAB放置于平面直角坐标系xOy中,C是AB边上的一个点(不与端点A、B重合),作CD⊥OB于点D,若点C、D都在双曲线y=$\frac{k}{x}$上(k>0,x>0),则k的值为( )
如图,将边长为2的等边△OAB放置于平面直角坐标系xOy中,C是AB边上的一个点(不与端点A、B重合),作CD⊥OB于点D,若点C、D都在双曲线y=$\frac{k}{x}$上(k>0,x>0),则k的值为( )| A. | $\frac{9}{16}$$\sqrt{3}$ | B. | $\frac{3}{4}$$\sqrt{3}$ | C. | $\frac{9}{25}$$\sqrt{3}$ | D. | $\frac{3}{5}$$\sqrt{3}$ |
20.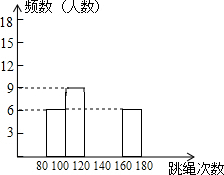 某校为了了解九年级学生(共450人)的身体素质情况,体育老师对九(1)班的50位学生进行一分钟跳绳次数测试,以测试数据为样本,绘制了如下部分频数分布表和部分频数分布直方图.
某校为了了解九年级学生(共450人)的身体素质情况,体育老师对九(1)班的50位学生进行一分钟跳绳次数测试,以测试数据为样本,绘制了如下部分频数分布表和部分频数分布直方图.
请结合图表解答下列问题:
(1)表中的m=12;
(2)请把频数分布直方图补完整;
(3)这个样本数据的中位数落在第三组;
(4)若九年级学生一分钟跳绳次数(x)合格要求是x≥120,则估计九年级学生中一分钟跳绳成绩不合格的人数.
 某校为了了解九年级学生(共450人)的身体素质情况,体育老师对九(1)班的50位学生进行一分钟跳绳次数测试,以测试数据为样本,绘制了如下部分频数分布表和部分频数分布直方图.
某校为了了解九年级学生(共450人)的身体素质情况,体育老师对九(1)班的50位学生进行一分钟跳绳次数测试,以测试数据为样本,绘制了如下部分频数分布表和部分频数分布直方图.| 组别 | 次数x | 频数(人数) |
| A | 80≤x<100 | 6 |
| B | 100≤x<120 | 8 |
| C | 120≤x<140 | m |
| D | 140≤x<160 | 18 |
| E | 160≤x<180 | 6 |
(1)表中的m=12;
(2)请把频数分布直方图补完整;
(3)这个样本数据的中位数落在第三组;
(4)若九年级学生一分钟跳绳次数(x)合格要求是x≥120,则估计九年级学生中一分钟跳绳成绩不合格的人数.
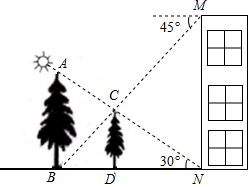 如图,在楼房MN前有两棵树与楼房在同一直线上,且垂直于地面,为了测量树AB、CD的高度,小明爬到楼房顶部M处,光线恰好可以经过树CD的顶站C点到达树AB的底部B点,俯角为45°,此时小亮测得太阳光线恰好经过树CD的顶部C点到达楼房的底部N点,与地面的夹角为30°,树CD的影长DN为15米,请求出树AB、CD的高度.(结果保留根号)
如图,在楼房MN前有两棵树与楼房在同一直线上,且垂直于地面,为了测量树AB、CD的高度,小明爬到楼房顶部M处,光线恰好可以经过树CD的顶站C点到达树AB的底部B点,俯角为45°,此时小亮测得太阳光线恰好经过树CD的顶部C点到达楼房的底部N点,与地面的夹角为30°,树CD的影长DN为15米,请求出树AB、CD的高度.(结果保留根号)