题目内容
15．
如图，在热气球上A处测得一栋大楼顶部B的俯角为23°，测得这栋大楼底部C的俯角为45°．已知热气球A处距地面的高度为180m，求这栋大楼的高度（精确到1m）．（参考数据：sin23°=0.39，cos23°=0.92，tan23°=0.42）
分析 首先过点A作直线BC的垂线，垂足为点D，进而求出CD的长，利用tan23°=$\frac{BD}{AD}$，得BD的长，即可得出答案．
解答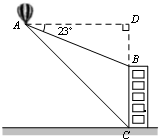 
解：过点A作直线BC的垂线，垂足为点D．
由题意，得∠CAD=45°，∠BAD=23°，CD=180．
∴∠CAD=∠ACD=45°．
∴CD=AD=180．
在Rt△ABD中，∠BDA=90°，$tan∠BAD=\frac{BD}{AD}=0.42$．
∴BD=0.42×180=75.6．
∴BC=CD-BD=180-75.6=104.4≈104m．
答：这栋大楼的高约为104m．
点评 此题主要考查了解直角三角形的应用，根据题意正确构造直角三角形是解题关键．
练习册系列答案
寒假乐园北京教育出版社系列答案
相关题目
5．某公司需招聘一名员工，对应聘者甲、乙、丙从笔试、面试、体能三个方面进行量化考核，三人各项得分如表：
（1）根据三项得分的平均分，从高到低确定三名应聘者的排名顺序．
（2）该公司规定：笔试，面试、体能得分分别不得低于80分，80分，70分，并按50%，30%，20%的比例计入总分．根据规定，请你说明谁将被录用．
| 笔试 | 面试 | 体能 | |
| 甲 | 84 | 78 | 90 |
| 乙 | 85 | 80 | 75 |
| 丙 | 80 | 90 | 73 |
（2）该公司规定：笔试，面试、体能得分分别不得低于80分，80分，70分，并按50%，30%，20%的比例计入总分．根据规定，请你说明谁将被录用．
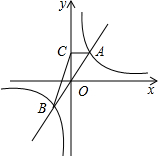如图，正比例函数y1=mx（m＞0）的图象与反比例函数y2=$\frac{k}{x}$（k≠0）的图象交于点A（n，4）和点B，AC⊥y轴，垂足为M，△ACB的面积为8．
