题目内容
6.红红有两把不同的锁和四把不同的钥匙,其中只有两把钥匙能打开对应的两把锁,用列表法或树状图求概率.(1)若取一把钥匙,求红红一次打开锁的概率.
(2)若取两把钥匙,求红红恰好打开两把锁的概率.
分析 (1)首先根据题意画出树状图,然后由树状图求得所有等可能的结果,进一步得到取一把钥匙,红红一次打开锁的概率;
(2)首先根据题意画出树状图,然后由树状图求得所有等可能的结果,进一步得到取两把钥匙,红红恰好打开两把锁的概率.
解答 解:(1)分别用A与B表示锁,用A、B、C、D表示钥匙,
画树状图得:
可得共有8种等可能的结果;
∵一次打开锁的有2种情况,
∴一次打开锁的概率为:$\frac{2}{8}$=$\frac{1}{4}$;
(2)分别用A、B、C、D表示钥匙,
画树状图得:
可得共有12种等可能的结果;
∵恰好打开两把锁的有2种情况,
∴恰好打开两把锁的概率为:$\frac{2}{12}$=$\frac{1}{6}$.
点评 本题考查的是用列表法或画树状图法求概率.列表法或画树状图法可以不重复不遗漏的列出所有可能的结果,列表法适合于两步完成的事件,树状图法适合两步或两步以上完成的事件.注意概率=所求情况数与总情况数之比.

练习册系列答案
相关题目
16.在一次概率实验中,用计算机从3,4,5,x这四个数中,每次同时随机抽取两个数,计算两数之和并记录,多次重复实验的数据如下表:
解答下列问题:
(1)如果实验继续进行下去,根据上表数据,出现“和为8”频率将稳定在它的概率附近.估计出现“和为8”的概率是0.33.
(2)当x值取6,求两数之和为8的概率.
| 实验总次数 | 10 | 20 | 30 | 60 | 90 | 120 | 180 | 240 | 330 | 450 |
| “和为8”出现频数 | 2 | 10 | 13 | 24 | 30 | 37 | 58 | 82 | 110 | 150 |
| “和为8”出现频率 | 0.20 | 0.50 | 0.43 | 0.38 | 0.33 | 0.31 | 0.32 | 0.34 | 0.33 | 0.33 |
(1)如果实验继续进行下去,根据上表数据,出现“和为8”频率将稳定在它的概率附近.估计出现“和为8”的概率是0.33.
(2)当x值取6,求两数之和为8的概率.
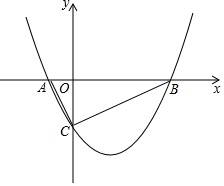 如图,抛物线y=$\frac{1}{2}$x2+bx-2与x轴相交于点A、B,与y轴相交于点C,且A(-1,0).
如图,抛物线y=$\frac{1}{2}$x2+bx-2与x轴相交于点A、B,与y轴相交于点C,且A(-1,0). 如图,在△ABC中,∠BAC=90°,AD是中线,E是AD的中点,过点A作AF∥BC交BE的延长线于F,连接CF.
如图,在△ABC中,∠BAC=90°,AD是中线,E是AD的中点,过点A作AF∥BC交BE的延长线于F,连接CF.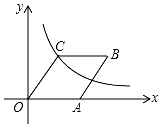 如图,在平面直角坐标系中,菱形OABC的顶点A在x轴的正半轴上,反比例函数y=$\frac{12}{x}$的图象经过点C(3,m).
如图,在平面直角坐标系中,菱形OABC的顶点A在x轴的正半轴上,反比例函数y=$\frac{12}{x}$的图象经过点C(3,m).