题目内容
8．
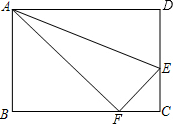如图，小刚用一张长方形纸片ABCD进行折纸，已知该纸片宽AB为4cm，长BC为5cm．当小刚折叠时，顶点D落在BC边上的点F处（折痕为AE），此时FC的长度是2cm．
分析 根据翻折变换的性质得到AF=AD=5cm，根据勾股定理求出BF，计算即可．
解答 解：由折叠的性质可知，AF=AD=5cm，
由勾股定理得，BF=$\sqrt{A{F}^{2}-A{B}^{2}}$=3，
则FC=5-3=2cm，
故答案为：2cm．
点评 本题考查的是翻折变换的性质，翻折变换是一种对称变换，它属于轴对称，折叠前后图形的形状和大小不变，位置变化，对应边和对应角相等．
练习册系列答案
相关题目
18．有两个一元二次方程：M：ax2+bx+c=0，N：cx2+bx+a=0，其中a+c=0，以下列四个结论中，错误的是（ ）
| A． | 如果方程M有两个不相等的实数根，那么方程N也有两个不相等的实数根 | |
| B． | 如果6是方程M的一个根，那么$\frac{1}{6}$是方程N的一个根 | |
| C． | 如果方程M和方程N有一个相同的根，那么这个根必是x=-1 | |
| D． | 如果方程M有两根符号相异，那么方程N的两根符号也相异 |
19．估计$\sqrt{11}$-1的值在（ ）
| A． | 1到2之间 | B． | 2到3之间 | C． | 3到4之间 | D． | 4到5之间 |
16．-（-32）的相反数是（ ）
| A． | 9 | B． | -9 | C． | 6 | D． | -6 |
3．在?ABCD中，下列结论一定正确的是（ ）
| A． | AC⊥BD | B． | ∠A+∠B=180° | C． | AB=AD | D． | BC∥CD |
13．1-（x-y）2化简后结果是（ ）
| A． | 1-x2+y2 | B． | 1-x2-y2 | C． | 1-x2-2xy+y2 | D． | 1-x2+2xy-y2 |
17．某商品原售价500元，经过连续两次降价后售价为400元．设平均每次降价的百分率为x，则下面所列方程中正确的是（ ）
| A． | 500（1-x）2=400 | B． | 400（1-x）2=500 | C． | 500（1-2x）=400 | D． | 400（1-2x）=500 |
