题目内容
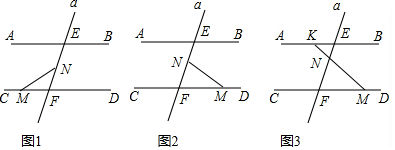
18.如图,已知AB∥CD,直线a分别交AB,CD于点E,F,点N在线段EF上,M是直线CD上的一个动点(点M与点F不重合)(1)如图1,当点M在射线FC上运动时,求证:∠FMN+∠ENM=∠AEF;
(2)如图2,当点M在射线FD上运动时,∠FMN,∠FNM和∠AEF三者的关系为∠AEF=180°-∠FMN-∠FNM(直接写出,不需证明)
(3)在(2)的条件下,如图3,延长MN交直线AB于点K,若∠AEF=60°,∠FMN:∠FNM=3:5,求∠AKM的度数
分析 利用平行线的性质及三角形的内角和定理分析求解.
解答 (1)证明:∵AB∥CD,直线a分别交AB,CD于点E、F,
∴∠AEF+∠EFC=180°
又在△FMN中,∠MFN+(∠FMN+∠FNM)=180°
∴∠FMN+∠FNM=∠AEF;
(2)解:∵AB∥CD,直线a分别交AB,CD于点E、F,
∴∠AEF=∠EFD,
而∠EFD=180°-∠FMN-∠FNM(三角形的内角和定理)
∴∠AEF=180°-∠FMN-∠FNM
(3)∵∠AEF=60°
∴∠EFM=60°,
∴∠FMN+∠FNM=120°,
又,∠FMN:∠FNM=3:5,
∴∠FMN=120°×$\frac{3}{8}$=45°
又∵AB∥CD,
∴∠AKM+∠FMN=180°,
∴∠AKM=180°-45°=135°
即:∠AKM的度数为135°
点评 本题考查了平行线的性质、三角形的内角和定理的等知识点,解题的关键是掌握平行线的性质.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
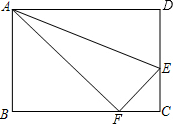 如图,小刚用一张长方形纸片ABCD进行折纸,已知该纸片宽AB为4cm,长BC为5cm.当小刚折叠时,顶点D落在BC边上的点F处(折痕为AE),此时FC的长度是2cm.
如图,小刚用一张长方形纸片ABCD进行折纸,已知该纸片宽AB为4cm,长BC为5cm.当小刚折叠时,顶点D落在BC边上的点F处(折痕为AE),此时FC的长度是2cm.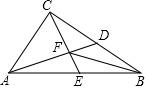 如图,在Rt△ABC中,∠ACB=90°,AD、CE分别是BC、AB边上的中线,且满足AD⊥CE,垂足为F,联结BF.
如图,在Rt△ABC中,∠ACB=90°,AD、CE分别是BC、AB边上的中线,且满足AD⊥CE,垂足为F,联结BF. 如图,∠MON=30°,点A1、A2、A3…在射线ON上,点B1、B2、B3…在射线OM上,△A1B1A2、△A2B2A3、△A3B3A4…均为等边三角形,依此类推,若OA1=1,则△A2016B2016A2017的边长为( )
如图,∠MON=30°,点A1、A2、A3…在射线ON上,点B1、B2、B3…在射线OM上,△A1B1A2、△A2B2A3、△A3B3A4…均为等边三角形,依此类推,若OA1=1,则△A2016B2016A2017的边长为( ) 如图,直角△ABC中,AB=5,BC=3,AC=4,直角△ABC将沿着它的一条边AB旋转一周,得到一个什么图形?试求出其表面积和点C运动的路程.
如图,直角△ABC中,AB=5,BC=3,AC=4,直角△ABC将沿着它的一条边AB旋转一周,得到一个什么图形?试求出其表面积和点C运动的路程.