题目内容
11.某商店售一种纪念品,已知成批购进时单价为4元,根据市场调查,销售量与销售单价在一段时间内满足如下关系:单价为10元时销售量为300枚,而单价每降低1元,就可多售出5枚,那么当销售单价为10元时,可以获得最大利润,最大利润为1800元.分析 根据总利润=销售数量×每件的利润就可以表示出利润y与x之间的函数关系式,由函数的性质就可以求出结论.
解答 解:由题意,得
y=(x-4)(300+$\frac{10-x}{1}×5$),(x≤10)
y=-5x2+370x-1400,
y=-5(x-37)2+5445,
∴a=-5<0,
∴x=37为对称轴时,在对称轴的左侧y随x的增大而增大.
∴当x=10时,y最大=1800元.
故答案为:10,1800.
点评 本题考查了销售问题的数量关系总利润=销售数量×每件的利润的运用,二次函数的性质的运用,解答时求出函数的解析式是关键.

练习册系列答案
 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
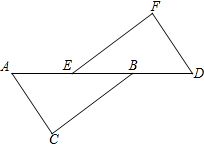 已知如图:AE=DB,∠C=∠F,BC∥EF,求证:△ABC≌△DEF.
已知如图:AE=DB,∠C=∠F,BC∥EF,求证:△ABC≌△DEF.