题目内容
7.设a=t+2,b=t+3,c=t+4,则a2+b2+c2-ab-ac-bc=3.分析 利用已知条件可得到a-b=-1,b-c=-1,c-a=2,再利用配方法得到原式=$\frac{1}{2}$[(a-b)2+(b-c)2+(c-a)2],然后利用整体代入的方法计算.
解答 解:∵a=t+2,b=t+3,c=t+4,
∴a-b=-1,b-c=-1,c-a=2,
∴a2+b2+c2-ab-ac-bc=$\frac{1}{2}$(2a2+2b2+2c2-2ab-2ac-2bc)
=$\frac{1}{2}$[(a-b)2+(b-c)2+(c-a)2]
=$\frac{1}{2}$[(-1)2+(-1)2+22]
=$\frac{1}{2}$(1+1+4)
=3.
故答案为3.
点评 本题考查了因式分解的应用:利用因式分解解决求值问题;利用因式分解解决证明问题;利用因式分解简化计算问题.

练习册系列答案
相关题目
2.知道风靡全球的魔方吗?它是匈牙利建筑学教授鲁比克为帮助学生增强空间思维能力而发明的教学工具,魔方的任何一面都可水平转动而不影响到其他方块.如图是一个三阶魔方,若将任何一面顺时针或逆时针旋转90°视作一次操作,那么由甲图到乙图至少需要进行这样的操作( )


| A. | 1次 | B. | 2次 | C. | 3次 | D. | 4次 |
19. 进入三月以来重庆的气温逐渐回暖,羽绒服进入了销售淡季.为此重庆新世纪百货对的某品牌的A款羽绒服进行了清仓大处理.已知A款羽绒服的销售价格y(元)与第x天(1≤x≤10,且x为整数)之间的关系可用如表表示:
进入三月以来重庆的气温逐渐回暖,羽绒服进入了销售淡季.为此重庆新世纪百货对的某品牌的A款羽绒服进行了清仓大处理.已知A款羽绒服的销售价格y(元)与第x天(1≤x≤10,且x为整数)之间的关系可用如表表示:
在销售的前6天A款羽绒服的销售数量z1(件)与第x天的关系式为z1=20x+40(1≤x≤6,且x为整数);后4天(7≤x≤10,且x为整数)的销售数量z2(件)与第x天的关系如图所示
(1)请观察题中的表格,用所学过的一次函数、反比例函数或二次函数的有关知识,直接写出y与x之间的函数关系式,根据如图所示的变化趋势,直接写出z2与x之间满足的一次函数关系式;
(2)若A款羽绒服的进价为每件200元,该专柜共有5个员工,每位员工每天的工资为100元.该专柜每天所需的固定支出为1000元,请结合上述信息,求出这10天内哪天的利润最大,并求出这个最大利润;
(3)在第(2)问的前提下,为了提高收益,减少库存,商场在第11天作出以下决定:第11~15天继续维持A款羽绒服的售价,结果每天的销售量均与第10天的持平;同时在第11~15天将B款羽绒服也作为促销商品,而且作为销售重点,已知B款羽绒服的进价仍为200元/件,销售价格比A款羽绒服取得最大利润当天的售价降低了a%,而每天销售量则比第10天A款羽绒服的销量提高了2a%.结果最后5天A、B两款羽绒服的总利润为27100元,请你参考以下数据,计算出a的值.
(参考数据:2.52=6.25,2.62=6.76,2.72=7.29,2.82=7.84)
 进入三月以来重庆的气温逐渐回暖,羽绒服进入了销售淡季.为此重庆新世纪百货对的某品牌的A款羽绒服进行了清仓大处理.已知A款羽绒服的销售价格y(元)与第x天(1≤x≤10,且x为整数)之间的关系可用如表表示:
进入三月以来重庆的气温逐渐回暖,羽绒服进入了销售淡季.为此重庆新世纪百货对的某品牌的A款羽绒服进行了清仓大处理.已知A款羽绒服的销售价格y(元)与第x天(1≤x≤10,且x为整数)之间的关系可用如表表示:| 时间x(天) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 售价y(元/件) | 550 | 500 | 450 | 400 | 350 | 300 | 300 | 300 | 300 | 300 |
(1)请观察题中的表格,用所学过的一次函数、反比例函数或二次函数的有关知识,直接写出y与x之间的函数关系式,根据如图所示的变化趋势,直接写出z2与x之间满足的一次函数关系式;
(2)若A款羽绒服的进价为每件200元,该专柜共有5个员工,每位员工每天的工资为100元.该专柜每天所需的固定支出为1000元,请结合上述信息,求出这10天内哪天的利润最大,并求出这个最大利润;
(3)在第(2)问的前提下,为了提高收益,减少库存,商场在第11天作出以下决定:第11~15天继续维持A款羽绒服的售价,结果每天的销售量均与第10天的持平;同时在第11~15天将B款羽绒服也作为促销商品,而且作为销售重点,已知B款羽绒服的进价仍为200元/件,销售价格比A款羽绒服取得最大利润当天的售价降低了a%,而每天销售量则比第10天A款羽绒服的销量提高了2a%.结果最后5天A、B两款羽绒服的总利润为27100元,请你参考以下数据,计算出a的值.
(参考数据:2.52=6.25,2.62=6.76,2.72=7.29,2.82=7.84)
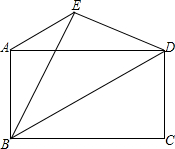 如图,已知矩形ABCD,把矩形ABCD沿直线BD翻折,点C落在点E处,连接AE.
如图,已知矩形ABCD,把矩形ABCD沿直线BD翻折,点C落在点E处,连接AE.