题目内容
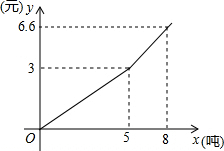 某自来水公司为了鼓励市民节约用水,采取分段收费标准,若某用户居民每月应交水费y(元)是用户量x(方)的函数,其图象如图所示,根据y(元)图象回答下列问题:
某自来水公司为了鼓励市民节约用水,采取分段收费标准,若某用户居民每月应交水费y(元)是用户量x(方)的函数,其图象如图所示,根据y(元)图象回答下列问题:(1)分别求出x≤5和x>5时,y与x的函数关系式;
(2)自来水公司的收费标准是什么?
(3)若某户居民交水费9元,该月用水多少方?
考点:一次函数的应用
专题:
分析:(1)根据图形可以写出两段解析式,
(2)由(1)即可求得自来水公司采取的收费标准,
(3)根据没有超过5吨,按0.6元每吨,超过5吨,超过部分按1.2元收费,求出即可.
(2)由(1)即可求得自来水公司采取的收费标准,
(3)根据没有超过5吨,按0.6元每吨,超过5吨,超过部分按1.2元收费,求出即可.
解答:解:(1)将(5,3)代入y=ax得:
5a=3,
解得:a=0.6,
故y=0.6x(x≤5),
将(5,3),(8,6.6)代入y=kx+b得:
,
解得:
故解析式为:y=1.2x-3(x>5);
(2)由(1)解析式得出:
x≤5自来水公司的收费标准是每吨0.6元.
x>5自来水公司的收费标准是每吨1.2元;
(3)若某户居民该月交水费9元,设用水x吨,0.6×5+1.2(x-5)=9,
解得:x=10,
则用水10吨.
5a=3,
解得:a=0.6,
故y=0.6x(x≤5),
将(5,3),(8,6.6)代入y=kx+b得:
|
解得:
|
故解析式为:y=1.2x-3(x>5);
(2)由(1)解析式得出:
x≤5自来水公司的收费标准是每吨0.6元.
x>5自来水公司的收费标准是每吨1.2元;
(3)若某户居民该月交水费9元,设用水x吨,0.6×5+1.2(x-5)=9,
解得:x=10,
则用水10吨.
点评:本题考查的是用一次函数解决实际问题,此类题是近年中考中的热点问题.注意利用一次函数求最值时,关键是应用一次函数的性质.

练习册系列答案
相关题目
如图几何体的俯视图为( )


A、 |
B、 |
C、 |
D、 |
 如图,矩形ABCD的顶点A、D在反比例函数
如图,矩形ABCD的顶点A、D在反比例函数 如图,直线L1:y=kx-4(k>0)与x轴、y轴分别交于点A、B,现将直线L1沿x轴正方向平移m个单位长度后得到直线L2,直线L2与x,y轴分别交于点C、D,已知两直线L1,L2之间的距离等于3.
如图,直线L1:y=kx-4(k>0)与x轴、y轴分别交于点A、B,现将直线L1沿x轴正方向平移m个单位长度后得到直线L2,直线L2与x,y轴分别交于点C、D,已知两直线L1,L2之间的距离等于3. 如图,已知菱形ABCD的对角线相交于点O,延长AB至点E,使BE=AB,连结CE.
如图,已知菱形ABCD的对角线相交于点O,延长AB至点E,使BE=AB,连结CE.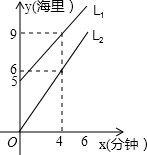 如图信息,l1为走私船,l2为我公安快艇,航行时路程与时间的函数图象,问
如图信息,l1为走私船,l2为我公安快艇,航行时路程与时间的函数图象,问