题目内容
 如图,直线L1:y=kx-4(k>0)与x轴、y轴分别交于点A、B,现将直线L1沿x轴正方向平移m个单位长度后得到直线L2,直线L2与x,y轴分别交于点C、D,已知两直线L1,L2之间的距离等于3.
如图,直线L1:y=kx-4(k>0)与x轴、y轴分别交于点A、B,现将直线L1沿x轴正方向平移m个单位长度后得到直线L2,直线L2与x,y轴分别交于点C、D,已知两直线L1,L2之间的距离等于3.(1)用含k的代数式表示m;
(2)若S△AB0:S四边形ABDC=1:3,试求点A坐标.
考点:一次函数图象与几何变换
专题:
分析:(1)先由直线L1的解析式为y=kx-4(k>0),得出L1与x轴、y轴的交点A、B的坐标,再根据平移的规律得出直线L2的解析式为y=k(x-m)-4,则L2与x,y轴的交点C、D的坐标可求.过A、B分别作L2的垂线段AE、BF,则AE=BF=3,由两角对应相等的两三角形相似得出△ACE∽△DBF,则
=
,即
=
,整理后即可得出用含k的代数式表示m的式子;
(2)先由AB∥CD,得出△ABO∽△CDO,根据相似三角形的性质得出S△AB0:S△CD0=(OA:OC)2=1:4,则OA:OC=1:2,由此列出方程m+
=2×
,进而得出m=
,再将m=
代入,求出k=
,即可得到点A的坐标.
| AC |
| DB |
| CE |
| BF |
| m |
| km |
| ||
| 3 |
(2)先由AB∥CD,得出△ABO∽△CDO,根据相似三角形的性质得出S△AB0:S△CD0=(OA:OC)2=1:4,则OA:OC=1:2,由此列出方程m+
| 4 |
| k |
| 4 |
| k |
| 4 |
| k |
3
| ||
| k |
| 7 |
| 9 |
解答: 解:(1)∵直线L1:y=kx-4(k>0)与x轴、y轴分别交于点A、B,
解:(1)∵直线L1:y=kx-4(k>0)与x轴、y轴分别交于点A、B,
∴A(
,0),B(0,-4).
∵将直线L1沿x轴正方向平移m个单位长度后得到直线L2,
∴直线L2的解析式为y=k(x-m)-4.
∵直线L2与x,y轴分别交于点C、D,
∴C(m+
,0),D(0,-km-4).
过A、B分别作L2的垂线段AE、BF,则AE=BF=3.
在△ACE与△DBF中,
,
∴△ACE∽△DBF,
∴
=
,即
=
,
整理,得m=
;
(2)∵S△AB0:S四边形ABDC=1:3,
∴S△AB0:S△CD0=1:4.
∵AB∥CD,
∴△ABO∽△CDO,
∴S△AB0:S△CD0=(OA:OC)2,
∴(OA:OC)2=1:4,
∴OA:OC=1:2,
∴OC=2OA,
∴m+
=2×
,
∴m=
,
∵m=
,
∴
=
,
解得k=
,
∴点A坐标为(
,0).
 解:(1)∵直线L1:y=kx-4(k>0)与x轴、y轴分别交于点A、B,
解:(1)∵直线L1:y=kx-4(k>0)与x轴、y轴分别交于点A、B,∴A(
| 4 |
| k |
∵将直线L1沿x轴正方向平移m个单位长度后得到直线L2,
∴直线L2的解析式为y=k(x-m)-4.
∵直线L2与x,y轴分别交于点C、D,
∴C(m+
| 4 |
| k |
过A、B分别作L2的垂线段AE、BF,则AE=BF=3.
在△ACE与△DBF中,
|
∴△ACE∽△DBF,
∴
| AC |
| DB |
| CE |
| BF |
| m |
| km |
| ||
| 3 |
整理,得m=
3
| ||
| k |
(2)∵S△AB0:S四边形ABDC=1:3,
∴S△AB0:S△CD0=1:4.
∵AB∥CD,
∴△ABO∽△CDO,
∴S△AB0:S△CD0=(OA:OC)2,
∴(OA:OC)2=1:4,
∴OA:OC=1:2,
∴OC=2OA,
∴m+
| 4 |
| k |
| 4 |
| k |
∴m=
| 4 |
| k |
∵m=
3
| ||
| k |
∴
3
| ||
| k |
| 4 |
| k |
解得k=
| 7 |
| 9 |
∴点A坐标为(
| 36 |
| 7 |
点评:本题考查了一次函数图象与几何变换,一次函数图象上点的坐标特征,相似三角形的判定与性质,综合性较强,有一定难度.

练习册系列答案
相关题目
 如图,点A、B在反比例函数y=
如图,点A、B在反比例函数y= 小明用自制的直角三角形纸板DEF测量树AB的高度.测量时,使直角边DE保持水平状态,其延长线交AB于点G;使斜边DF与点A在同一条直线上.测得边DE离地面的高度GB为1.4m,点D到AB的距离DG为6m(如图).已知DE=30cm,EF=20cm,那么树AB的高度等于( )
小明用自制的直角三角形纸板DEF测量树AB的高度.测量时,使直角边DE保持水平状态,其延长线交AB于点G;使斜边DF与点A在同一条直线上.测得边DE离地面的高度GB为1.4m,点D到AB的距离DG为6m(如图).已知DE=30cm,EF=20cm,那么树AB的高度等于( )
 如图,在一个坡角为15°的斜坡上有一棵树,高为AB.当太阳光与水平线成50°时,测得该树在斜坡上的树影BC的长为7米,求树高.(精确到0.1m)(参考数据:sin15°≈0.26,cos15°≈0.97,tan15°≈0..27,sin50°≈0.77,cos50°≈0.64,tan50≈1.19)
如图,在一个坡角为15°的斜坡上有一棵树,高为AB.当太阳光与水平线成50°时,测得该树在斜坡上的树影BC的长为7米,求树高.(精确到0.1m)(参考数据:sin15°≈0.26,cos15°≈0.97,tan15°≈0..27,sin50°≈0.77,cos50°≈0.64,tan50≈1.19)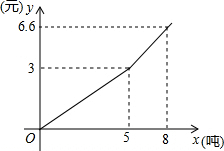 某自来水公司为了鼓励市民节约用水,采取分段收费标准,若某用户居民每月应交水费y(元)是用户量x(方)的函数,其图象如图所示,根据y(元)图象回答下列问题:
某自来水公司为了鼓励市民节约用水,采取分段收费标准,若某用户居民每月应交水费y(元)是用户量x(方)的函数,其图象如图所示,根据y(元)图象回答下列问题: