题目内容
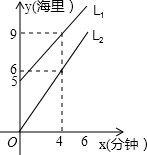 如图信息,l1为走私船,l2为我公安快艇,航行时路程与时间的函数图象,问
如图信息,l1为走私船,l2为我公安快艇,航行时路程与时间的函数图象,问(1)在刚出发时我公安快艇距走私船多少海里?
(2)计算走私船与公安快艇的速度分别是多少?
(3)分别求出l1,l2的解析式.
考点:一次函数的应用
专题:
分析:(1)观察图形直接得出两船的距离;
(2)利用两船行驶的距离与时间即可得出其速度;
(3)利用待定系数法求一次函数解析式即可.
(2)利用两船行驶的距离与时间即可得出其速度;
(3)利用待定系数法求一次函数解析式即可.
解答:解:(1)由图象可得出:在刚出发时我公安快艇距走私船5海里;
(2)公安快艇是4分钟6海里,走私船是每分钟
=1海里;
公安快艇的速度是
=
(海里).
(3)设l1:y1=k1x+b过(0,5)和(4,9)点
则
,
解得:
,
∴y1=x+5
设l2:y2=k2x过(4,6)点,
∴y2=
x.
(2)公安快艇是4分钟6海里,走私船是每分钟
| 9-5 |
| 4 |
公安快艇的速度是
| 6 |
| 4 |
| 3 |
| 2 |
(3)设l1:y1=k1x+b过(0,5)和(4,9)点
则
|
解得:
|
∴y1=x+5
设l2:y2=k2x过(4,6)点,
∴y2=
| 3 |
| 2 |
点评:本题考查了识别函数图象的能力,观察图象提供的信息,再分析求解是解题关键.

练习册系列答案
相关题目
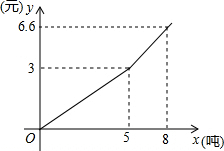 某自来水公司为了鼓励市民节约用水,采取分段收费标准,若某用户居民每月应交水费y(元)是用户量x(方)的函数,其图象如图所示,根据y(元)图象回答下列问题:
某自来水公司为了鼓励市民节约用水,采取分段收费标准,若某用户居民每月应交水费y(元)是用户量x(方)的函数,其图象如图所示,根据y(元)图象回答下列问题: 如图,如果把四边形ABCD沿EF折叠,使点A,B落在四边形EFCD内,试探究∠A+∠B与∠1+∠2之间存在着怎样的数量关系,证明你的结论.
如图,如果把四边形ABCD沿EF折叠,使点A,B落在四边形EFCD内,试探究∠A+∠B与∠1+∠2之间存在着怎样的数量关系,证明你的结论.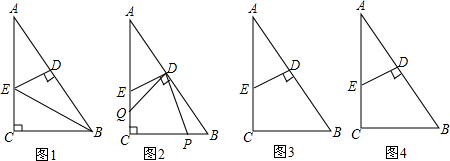
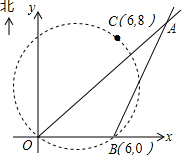 在某张航海图上,标明了三个观测点的坐标,如图,O(0,0)、B(6,0)、C(6,8),由三个观测点确定的圆形区域是海洋生物保护区.
在某张航海图上,标明了三个观测点的坐标,如图,O(0,0)、B(6,0)、C(6,8),由三个观测点确定的圆形区域是海洋生物保护区. 二次函数y=ax2+bx+c的图象过点(0,-3),(4,3),(2,-2).
二次函数y=ax2+bx+c的图象过点(0,-3),(4,3),(2,-2).