题目内容
10.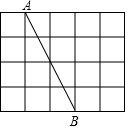 如图,在每个小正方形的边长为1的网格中,点A,B均在格点上.
如图,在每个小正方形的边长为1的网格中,点A,B均在格点上.(Ⅰ)线段AB的长为2$\sqrt{5}$.
(Ⅱ)请利用网格,用无刻度的直尺在AB上作出点P,使AP=$\frac{4\sqrt{5}}{3}$,并简要说明你的作图方法(不要求证明).取格点M,N,连接MN交AB于P,则点P即为所求.
分析 利用勾股定理列式求出AB=2$\sqrt{5}$,然后作一小正方形对角线,使对角线与AB的交点满足AP:BP=2:1即可.
解答  解:(1)由勾股定理得,AB=$\sqrt{{4}^{2}+{2}^{2}}$=2$\sqrt{5}$;
解:(1)由勾股定理得,AB=$\sqrt{{4}^{2}+{2}^{2}}$=2$\sqrt{5}$;
(2)∵AB=2$\sqrt{5}$,
所以,AP=$\frac{4\sqrt{5}}{3}$时AP:BP=2:1.
点P如图所示.取格点M,N,连接MN交AB于P,则点P即为所求;
故答案为:取格点M,N,连接MN交AB于P,则点P即为所求.
点评 本题考查了应用与设计作图,考虑利用相似三角形对应边成比例的性质是解题的关键.

练习册系列答案
 53天天练系列答案
53天天练系列答案
相关题目
15. 如图,平行四边形ABCD的顶点A,B,D在⊙O上,顶点C在⊙O的直径BE上,∠ADC=54°,连接AE,则∠AEB的度数为( )
如图,平行四边形ABCD的顶点A,B,D在⊙O上,顶点C在⊙O的直径BE上,∠ADC=54°,连接AE,则∠AEB的度数为( )
 如图,平行四边形ABCD的顶点A,B,D在⊙O上,顶点C在⊙O的直径BE上,∠ADC=54°,连接AE,则∠AEB的度数为( )
如图,平行四边形ABCD的顶点A,B,D在⊙O上,顶点C在⊙O的直径BE上,∠ADC=54°,连接AE,则∠AEB的度数为( )| A. | 36° | B. | 46° | C. | 27° | D. | 63° |
2.-8的相反数是( )
| A. | 8 | B. | -$\frac{1}{8}$ | C. | $\frac{1}{8}$ | D. | -8 |
 如图,矩形ABCD的对角线AC,BD相交于点O,若AB=3,OC=2.5,则BC长为4.
如图,矩形ABCD的对角线AC,BD相交于点O,若AB=3,OC=2.5,则BC长为4.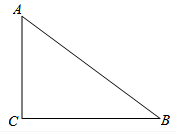 如图,已知Rt△ABC中,∠ACB=90°.请完成以下任务.
如图,已知Rt△ABC中,∠ACB=90°.请完成以下任务.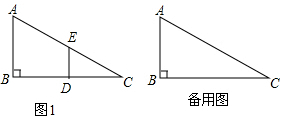 如图1,在Rt△ABC中,∠B=90°,BC=2AB=8,点D、E分别是边BC、AC的中点,连接DE,将△EDC绕点C按顺时针方向旋转,记旋转角为α.
如图1,在Rt△ABC中,∠B=90°,BC=2AB=8,点D、E分别是边BC、AC的中点,连接DE,将△EDC绕点C按顺时针方向旋转,记旋转角为α.