题目内容
16.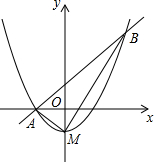 如图,顶点M(0,-1)在y轴上的抛物线与直线y=x+1相交于A,B两点,且点A在x轴上,连结AM,BM.
如图,顶点M(0,-1)在y轴上的抛物线与直线y=x+1相交于A,B两点,且点A在x轴上,连结AM,BM.(1)求点A的坐标和这个抛物线所表示的二次函数的表达式;
(2)求点B的坐标;
(3)把抛物线与直线y=x的交点称为抛物线的不动点.若将(1)中抛物线平移,使其顶点为(m,2m),当m满足什么条件时,平移后的抛物线总有不动点?
分析 (1)由点A是直线y=x+1与x轴的交点可求出点A的坐标,将抛物线的解析式设成顶点式,然后把点A的坐标代入该解析式,就可解决问题;
(2)只需解直线与抛物线的解析式组成的方程组,然后解这个方程组就可解决问题;
(3)将平移后的抛物线的解析式设成顶点式,然后把y=x代入该解析式,得到关于x的一元二次方程,要使平移后的抛物线总有不动点,只需该一元二次方程的根的判别式大于等于0即可.
解答 解:∵点A是直线y=x+1与x轴的交点,
∴A(-1,0).
设顶点为(0,-1)的抛物线的解析式为y=ax2-1,
∵点A(-1,0)在抛物线y=ax2-1上,
∴0=a-1,
∴a=1,
∴抛物线的解析式为y=x2-1;
(2)解方程组$\left\{\begin{array}{l}{y=x+1}\\{y={x}^{2}-1}\end{array}\right.$,得$\left\{\begin{array}{l}{{x}_{1}=-1}\\{{y}_{1}=0}\end{array}\right.$,$\left\{\begin{array}{l}{{x}_{2}=2}\\{{y}_{2}=3}\end{array}\right.$,
故点B的坐标为(2,3);
(3)设平移后的抛物线的解析式为y=(x-m)2+2m,
把y=x代入y=(x-m)2+2m,得
x=(x-m)2+2m,
整理得,x2-(2m+1)x+m2+2m=0,
由题可得△=(2m+1)2-4×1×(m2+2m)=1-4m≥0,
解得m≤$\frac{1}{4}$.
故当m≤$\frac{1}{4}$时,平移后的抛物线总有不动点.
点评 本题主要考查了直线上点的坐标特征、运用待定系数法求抛物线的解析式、求直线与抛物线的解析式的交点、根的判别式等知识,通常可将直线与抛物线的交点问题转化为一元二次方程解的问题.

| 购物总金额(原价) | 折扣率 |
| 不超过3000元的部分 | 九折 |
| 超过3000元但不超过5000元的部分 | 八折 |
| 超过5000元的部分 | 七折 |
(2)已知张老师购买了两件物品(一个冰箱和一个空调)共付费4060元.请问这两件物品的原价总共是多少元?
(3)碰巧同一天赵老师也在同一家专卖店购买了同样的两件物品.但赵老师上午去购买的冰箱,下 午去购买的空调,如此一来赵老师两次付款总额比张老师多花费了140元.已知此冰箱的原价比空调的原价要贵,求这两件物品的原价分别为多少元?
| A. | -3 | B. | 0 | C. | -2 | D. | 1 |
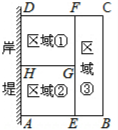 为了节省材料,某水产养殖户利用水库的岸堤(岸堤足够长)为一边,用总长为80m的围网在水库中围成了如图所示的①②③三块长方形区域,而且这三块长方形区域的面积相等.设BC的长度为xm,AB为ym.
为了节省材料,某水产养殖户利用水库的岸堤(岸堤足够长)为一边,用总长为80m的围网在水库中围成了如图所示的①②③三块长方形区域,而且这三块长方形区域的面积相等.设BC的长度为xm,AB为ym.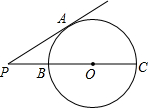 如图,PA切⊙O于点A,PC过点O且交⊙O于点B,C,若PA=2$\sqrt{3}$,PB=2,则⊙O的半径为2.
如图,PA切⊙O于点A,PC过点O且交⊙O于点B,C,若PA=2$\sqrt{3}$,PB=2,则⊙O的半径为2.