题目内容
8．
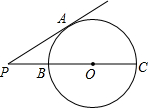如图，PA切⊙O于点A，PC过点O且交⊙O于点B，C，若PA=2$\sqrt{3}$，PB=2，则⊙O的半径为2．
分析 先由切割线定理知：AP2=PB•PC，可求出PC=6，则BC=PC-PB=4，进而可求出半径OC=2．
解答 解：∵PA切⊙O于A割线PBC过圆心，交⊙O于B、C，
∴AP2=PB•PC；
又∵PA=2$\sqrt{3}$，PB=2；
∴PC=6，
∴BC=4，
∴OC=2．
故答案为：2．
点评 本题主要考查了圆切割线定理，关键是根据切割线定理知：AP2=PB•PC解答．
练习册系列答案
相关题目
如图，平行四边形ABCD的对角线交于点O，且AB=5，△OCD的周长为23，则平行四边形ABCD的两条对角线的和是36．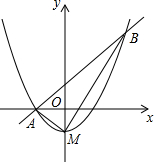
如图，顶点M（0，-1）在y轴上的抛物线与直线y=x+1相交于A，B两点，且点A在x轴上，连结AM，BM．
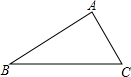已知：如图△ABC，∠ACB=2∠B=60°，BC=4．请按要求进行尺规作图，作∠ACB的平分线交AB于点D，再过点D作DE⊥BC，垂足为E，并求出AD的长．（不写作法，保留作图痕迹）．
20．
△ABC在直角坐标系中的位置如图所示，若将△ABC绕点O旋转，点C的对应点为点D，其中A（1，2），B（-1，0），C（3，-1），D（-1，-3），则旋转后点A的对应点E的坐标为（ ）
△ABC在直角坐标系中的位置如图所示，若将△ABC绕点O旋转，点C的对应点为点D，其中A（1，2），B（-1，0），C（3，-1），D（-1，-3），则旋转后点A的对应点E的坐标为（ ）| A． | （-1，2） | B． | （0，-1） | C． | （1，-3） | D． | （2，-1） |
17．下列说法正确的是（ ）
| A． | $\sqrt{4}$是无理数 | B． | $\sqrt{16}$的平方根是±4 | C． | 0的相反数是0 | D． | -0.5的倒数是2 |