题目内容
6.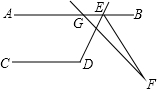 如图,已知AB∥CD,∠CDE=118°,直线GF与AB交于点G,与∠BED的平分线交于点F,若∠AGF=132°,则∠F的度数为( )
如图,已知AB∥CD,∠CDE=118°,直线GF与AB交于点G,与∠BED的平分线交于点F,若∠AGF=132°,则∠F的度数为( )| A. | 24° | B. | 12° | C. | 11° | D. | 10° |
分析 先根据平行线的性质求出∠AED与∠DEB的度数,再由角平分线的性质求出∠DEF的度数,进而可得出∠GEF的度数,再根据三角形外角的性质即可得出结论.
解答  解:∵AB∥CD,∠CDE=118°,
解:∵AB∥CD,∠CDE=118°,
∴∠AED=180°-118°=62°,∠DEB=118°.
∵GF交∠DEB的平分线EF于点F,
∴∠DEF=$\frac{1}{2}$×118°=59°,
∴∠GEF=62°+59°=121°.
∵∠AGF=132°,
∴∠F=∠AGF-∠GEF=132°-121°=11°.
故选:C.
点评 本题考查的是平行线的性质,解题时注意:两直线平行,同旁内角互补,内错角相等.

练习册系列答案
相关题目
14. 如图,MN是⊙O的直径,MN=8,∠AMN=40°,点B为弧AN的中点,点P是直径MN上的一个动点,则PA+PB的最小值为( )
如图,MN是⊙O的直径,MN=8,∠AMN=40°,点B为弧AN的中点,点P是直径MN上的一个动点,则PA+PB的最小值为( )
 如图,MN是⊙O的直径,MN=8,∠AMN=40°,点B为弧AN的中点,点P是直径MN上的一个动点,则PA+PB的最小值为( )
如图,MN是⊙O的直径,MN=8,∠AMN=40°,点B为弧AN的中点,点P是直径MN上的一个动点,则PA+PB的最小值为( )| A. | $\sqrt{3}$ | B. | 2$\sqrt{3}$ | C. | 3$\sqrt{3}$ | D. | 4$\sqrt{3}$ |
18.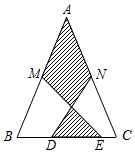 如图,在△ABC中,AB=AC,M,N分别是AB,AC的中点,D,E为BC上的点,连结DN,EM.若AB=13cm,BC=10cm,DE=5cm,则图中阴影部分面积为( )cm2.
如图,在△ABC中,AB=AC,M,N分别是AB,AC的中点,D,E为BC上的点,连结DN,EM.若AB=13cm,BC=10cm,DE=5cm,则图中阴影部分面积为( )cm2.
 如图,在△ABC中,AB=AC,M,N分别是AB,AC的中点,D,E为BC上的点,连结DN,EM.若AB=13cm,BC=10cm,DE=5cm,则图中阴影部分面积为( )cm2.
如图,在△ABC中,AB=AC,M,N分别是AB,AC的中点,D,E为BC上的点,连结DN,EM.若AB=13cm,BC=10cm,DE=5cm,则图中阴影部分面积为( )cm2.| A. | 25 | B. | 35 | C. | 30 | D. | 42 |
15. 如图,在平面直角坐标系中,反比例函数y=$\frac{8}{x}$(x>0)的图象交矩形OABC的边AB于点D,交边BC于点E,且BE=EC,四边形ODBE的面积为( )
如图,在平面直角坐标系中,反比例函数y=$\frac{8}{x}$(x>0)的图象交矩形OABC的边AB于点D,交边BC于点E,且BE=EC,四边形ODBE的面积为( )
 如图,在平面直角坐标系中,反比例函数y=$\frac{8}{x}$(x>0)的图象交矩形OABC的边AB于点D,交边BC于点E,且BE=EC,四边形ODBE的面积为( )
如图,在平面直角坐标系中,反比例函数y=$\frac{8}{x}$(x>0)的图象交矩形OABC的边AB于点D,交边BC于点E,且BE=EC,四边形ODBE的面积为( )| A. | 6 | B. | 7 | C. | 8 | D. | 12 |
16.据调查,某班20位女同学所穿鞋子的尺码如表所示,则鞋子尺码的众数和中位数分别是( )
| 尺码(码) | 34 | 35 | 36 | 37 | 38 |
| 人数 | 2 | 5 | 10 | 2 | 1 |
| A. | 35码,35码 | B. | 35码,36码 | C. | 36码,35码 | D. | 36码,36码 |
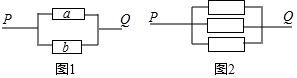 在物理实验中,当电流在一定时间段内正常通过电子元件时,每个电子元件的状态有两种可能;通电或断开,并且这种状态的可能性相等.
在物理实验中,当电流在一定时间段内正常通过电子元件时,每个电子元件的状态有两种可能;通电或断开,并且这种状态的可能性相等.
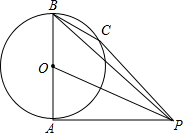 如图,AB为⊙O的直径,过⊙O外一点P作圆的两条切线,切点分别为点A和点C,连接BC和OP.
如图,AB为⊙O的直径,过⊙O外一点P作圆的两条切线,切点分别为点A和点C,连接BC和OP.