题目内容
已知：如图，在△ABC中，AB=AC，AD⊥BC，垂足为D，E为AC上一点，且DE∥AB，求证：∠ADE=∠DAE．考点：等腰三角形的判定与性质
专题：证明题
分析：已知AB=AC，AD⊥BC，易证∠BAD=∠CAD，根据平行线的性质证得∠ADE=∠BAD，进而证得∠ADE=∠DAE．
解答：证明：∵AB=AC，AD⊥BC，
∴∠BAD=∠CAD，
∵DE∥AB，
∴∠ADE=∠BAD，
∴∠ADE=∠CAD，
即∠ADE=∠DAE；
∴∠BAD=∠CAD，
∵DE∥AB，
∴∠ADE=∠BAD，
∴∠ADE=∠CAD，
即∠ADE=∠DAE；
点评：此题考查等腰三角形的性质和平行线的性质；等腰三角形底边上的高、中线、顶角的平分线三线合一，是经常用到的知识点．
练习册系列答案
相关题目
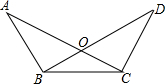如图所示，已知△ABC≌△DCB，∠A=32°，∠BCD=115°，求∠BOC．
如图，AD是△ABC（AB＞AC）的角平分线，AD的中垂线和BC的延长线交于点E，求证：DE2=BE•CE．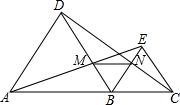
如图，A、B、C在同一直线上，且△ABD，△BCE都是等边三角形，AE交BD于点M，CD交BE于点N，求证：