Question

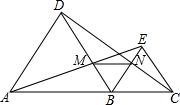如图，A、B、C在同一直线上，且△ABD，△BCE都是等边三角形，AE交BD于点M，CD交BE于点N，求证：
（1）∠BDN=∠BEM；
（2）△BMN是等边三角形．

Answer 1

考点：全等三角形的判定与性质,等边三角形的判定与性质

专题：证明题

分析：（1）由△ABD与△BCE都为等边三角形，利用等边三角形的性质得到两条边对应相等，两个角相等都为60°，利用SAS即可得到△ABE与△DBC全等，进而得到∠BDN=∠BEM；
（2）由第一问△ABE与△DBC全等，利用全等三角形的对应角相等得到一对角相等，再由∠ABD=∠EBC=60°，利用平角的定义得到∠MBE=∠NBC=60°，再由EB=CB，利用ASA可得出△EMB与△CNB全等，利用全等三角形的对应边相等得到MB=NB，再由∠MBE=60°，利用有一个角为60°的等腰三角形为等边三角形可得出△BMN为等边三角形．

解答：证明：（1）∵等边△ABD和等边△BCE，
∴AB=DB，BE=BC，∠ABD=∠EBC=60°，
∴∠ABE=∠DBC=120°，
在△ABE和△DBC中，

AB=DB   ∠ABE=∠DBC   BE=BC

，
∴△ABE≌△DBC（SAS）
∴∠BDN=∠BEM；
（2）∵△ABE≌△DBC，
∴∠AEB=∠DCB，
又∵∠ABD=∠EBC=60°，
∴∠MBE=180°-60°-60°=60°，
即∠MBE=∠NBC=60°，
在△MBE和△NBC中，

∠AEB=∠DCB   EB=CB   ∠MBE=∠NBC

，
∴△MBE≌△NBC（ASA），
∴BM=BN，∠MBE=60°，
∴△BMN为等边三角形．

点评：此题考查了等边三角形的判定与性质，以及全等三角形的判定与性质，熟练掌握判定与性质是解本题的关键．同时做第二问时注意利用第一问已证的结论．