题目内容
已知一次函数y=-x+
与x轴,y轴分别交于点A,B,直线l经过点O,且l∥AB,点F在l上,且AF=AB,则OF= .
| 2 |
考点:一次函数图象上点的坐标特征,等腰三角形的判定
专题:
分析:先求得交点坐标,得出两平行线之间的距离为1,分两种情况得出OF的长.
解答:解:∵一次函数y=-x+
与x轴,y轴分别交于点A,B,
∴点A(
,0),B(0,
),
∴AB=2,
∵l∥AB,
∴l的解析式为:y=-x,
∵AF=AB,
当点F在第四象限时,
∴OF=
+1,
当点F在第二象限时,
∴OF=
-1,
故答案为
±1.
| 2 |
∴点A(
| 2 |
| 2 |
∴AB=2,
∵l∥AB,
∴l的解析式为:y=-x,
∵AF=AB,
当点F在第四象限时,
∴OF=
| 3 |
当点F在第二象限时,
∴OF=
| 3 |
故答案为
| 3 |
点评:本题考查了一次函数图象上点的坐标特点以及等腰三角形的判定,是基础知识要熟练掌握.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
下列运算正确的是( )
| A、x3+x3=2x6 |
| B、x3•x2=x5 |
| C、(-3x3)2=3x6 |
| D、x6÷x2=x3 |
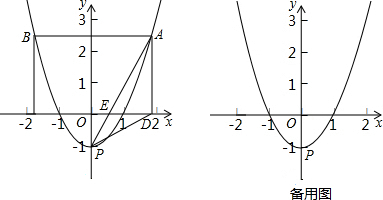
 如图,在△ABC中,点D、E分别在AB、BC上,且DE∥AC,若△ABC的面积是△BDE面积的两倍,则AC:DE=
如图,在△ABC中,点D、E分别在AB、BC上,且DE∥AC,若△ABC的面积是△BDE面积的两倍,则AC:DE=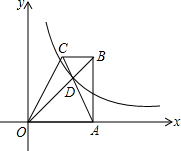 已知直角梯形ABCO的底边AO在x轴上,BC∥AO,AB⊥AO,对角线AC、BO相交于点D,双曲线y=
已知直角梯形ABCO的底边AO在x轴上,BC∥AO,AB⊥AO,对角线AC、BO相交于点D,双曲线y=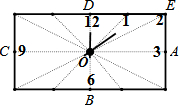 如图,艺术节期间我班数学兴趣小组设计了一只长方形时钟作品,其中心为O,数字3,6,9,12标在各边中点上,数字2在长方形顶点上,则数字1应该标在
如图,艺术节期间我班数学兴趣小组设计了一只长方形时钟作品,其中心为O,数字3,6,9,12标在各边中点上,数字2在长方形顶点上,则数字1应该标在