题目内容
2.若x2-4x-1=0,试求x-$\frac{1}{x}$,x2+$\frac{1}{{x}^{2}}$,$\frac{{x}^{2}}{{x}^{4}+{x}^{2}+1}$的值.分析 把已知等式两边除以x可得到x-$\frac{1}{x}$=4,再利用完全平方公式变形得到x2+$\frac{1}{{x}^{2}}$=(x-$\frac{1}{x}$)2+2,然后利用整体代入的方法计算,然后把$\frac{{x}^{2}}{{x}^{4}+{x}^{2}+1}$变形为$\frac{1}{{x}^{2}+1+\frac{1}{{x}^{2}}}$,然后利用整体代入的方法.
解答 解:∵x2-4x-1=0,
∴x-4-$\frac{1}{x}$=0,
∴x-$\frac{1}{x}$=4,
x2+$\frac{1}{{x}^{2}}$=(x-$\frac{1}{x}$)2+2=16+2=18,
$\frac{{x}^{2}}{{x}^{4}+{x}^{2}+1}$=$\frac{1}{{x}^{2}+1+\frac{1}{{x}^{2}}}$=$\frac{1}{18+1}$=$\frac{1}{19}$.
点评 本题考查了一元二次方程的解:能使一元二次方程左右两边相等的未知数的值是一元二次方程的解.

练习册系列答案
 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案
相关题目
12.下列说法正确的是( )
| A. | 两个等边三角形一定全等 | B. | 形状相同的两个三角形全等 | ||
| C. | 面积相等的两个三角形全等 | D. | 全等三角形的面积一定相等 |
12.在践行社会主义核心价值观活动中,共评选出各级各类“湖北好人”45 000多名.45 000这个数用科学记数法表示为( )
| A. | 4.5×103 | B. | 4.5×104 | C. | 4.5×105 | D. | 0.45×105 |
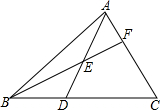 在△ABC中,D在BC上,E在AD上,连结BE,并延长交AC于F,若3BD=2CD,AE=DE,则$\frac{AF}{FC}$=$\frac{2}{5}$.
在△ABC中,D在BC上,E在AD上,连结BE,并延长交AC于F,若3BD=2CD,AE=DE,则$\frac{AF}{FC}$=$\frac{2}{5}$.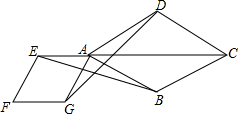 如图,点E是菱形ABCD对角线CA的延长线上任意一点,以线段AE为边作一个菱形AEFG,且∠EAG=∠BAD,连接EC,CD.
如图,点E是菱形ABCD对角线CA的延长线上任意一点,以线段AE为边作一个菱形AEFG,且∠EAG=∠BAD,连接EC,CD.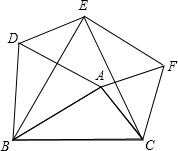 如图,已知△ABD,△BCE,△ACF都是等边三角形,求证:四边形ADEF是平行四边形.
如图,已知△ABD,△BCE,△ACF都是等边三角形,求证:四边形ADEF是平行四边形.