题目内容
16.设a、b、c都是实数,求证:(b-c)2≥(a-2b)(2c-a).分析 计算(b-c)2与(a-2b)(2c-a)的差,如果大于等于0,则:(b-c)2≥(a-2b)(2c-a);如果小于0,则:(b-c)2<(a-2b)(2c-a).
解答 证明:∵(b-c)2-(a-2b)(2c-a),
=b2-2bc+c2-2ac+a2+4bc-2ab,
=a2+b2+c2-2ac+2bc-2ab,
=b2+2bc+b2-2ac-2ab+a2,
=(b+c)2-2a(b+c)+a2,
=(b+c-a)2,
∵(b+c-a)2≥0,
∴(b-c)2-(a-2b)(2c-a)≥0,
∴(b-c)2≥(a-2b)(2c-a).
点评 本题是利用因式分解解决证明问题,考查了因式分解的应用和大小比较问题;具体做法是:根据题目的特点,利用求差法进行列式,通过因式分解将式子变形,变成完全平方式,从而得出结论.

练习册系列答案
相关题目
3.正整数按如图的规律排列,请写出第15行,第17列的数字是( )


| A. | 271 | B. | 270 | C. | 256 | D. | 255 |
1.若58-1能被20至30之间的两个整数整除,则这两个整数是( )
| A. | 22和24 | B. | 23和25 | C. | 24和26 | D. | 26和28 |
5.下列运算有错误的是( )
| A. | $\frac{1}{3}$÷(-3)=3×(-3) | B. | (-5)÷(-$\frac{1}{2}$)=-5×(-2) | C. | 5-(-2)=5+2 | D. | 2-3=(+2)+(-3) |
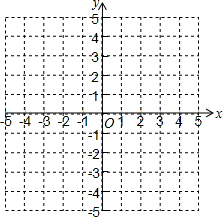 如图,在平面直角坐标系xOy中,已知点P(-1,0),C($\sqrt{2}$-1,1),D(0,-3),A,B在x轴上,且P为AB中点,S△CAP=1.
如图,在平面直角坐标系xOy中,已知点P(-1,0),C($\sqrt{2}$-1,1),D(0,-3),A,B在x轴上,且P为AB中点,S△CAP=1.