题目内容
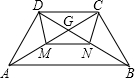 如图,在梯形ABCD中,AB∥CD,并且AB=2CD,M、N分别是对角线AC,BD的中点,设梯形ABCD的周长为L1,四边形CDMN的周长为L2,求L1:L2.
如图,在梯形ABCD中,AB∥CD,并且AB=2CD,M、N分别是对角线AC,BD的中点,设梯形ABCD的周长为L1,四边形CDMN的周长为L2,求L1:L2.考点:梯形,全等三角形的判定与性质,平行四边形的判定与性质
专题:计算题
分析:要求的两个四边形已经有AB=2CD,所以再寻求其它的边的关系,根据条件中的中点及角的关系先推出三角形全等,然后再结合条件和图形推出边的关系即可.
解答:解:如图所示,延长DM交AB于H,
设CD=x,则AB=2x,
∵M是AC的中点,
∴AM=CM,
∵AB∥CD,
∴∠DCM=∠HAM,
在△AMH和△CMD中,
,
∴△AMH≌△CMD(AAS),
∴DM=HM,DC=AH,
∵N是BD的中点,
∴DN=BN,
∴MN=
BH=
(AB-CD)=
x,
∵AB=2CD,
∴AB=2AH,
∴AH=HB,
∴CD=HB,
∴四边形DHBC是平行四边形,
∴DH=BC=2DM,
同理可得AD=2CN,
∴L1=AB+CD+AD+BC=2x+x+2DM+2CN=3x+2DM+2CN,
L2=MN+CD+DM+CN=
x+x+DM+CN=
x+DM+CN,
∴L1:L2=2:1.

设CD=x,则AB=2x,
∵M是AC的中点,
∴AM=CM,
∵AB∥CD,
∴∠DCM=∠HAM,
在△AMH和△CMD中,
|
∴△AMH≌△CMD(AAS),
∴DM=HM,DC=AH,
∵N是BD的中点,
∴DN=BN,
∴MN=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∵AB=2CD,
∴AB=2AH,
∴AH=HB,
∴CD=HB,
∴四边形DHBC是平行四边形,
∴DH=BC=2DM,
同理可得AD=2CN,
∴L1=AB+CD+AD+BC=2x+x+2DM+2CN=3x+2DM+2CN,
L2=MN+CD+DM+CN=
| 1 |
| 2 |
| 3 |
| 2 |
∴L1:L2=2:1.

点评:该题目考查了梯形的性质、三角形全等的判定和性质,关键是分析作出辅助线并推出四边形DHBC是平行四边形.

练习册系列答案
 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
从数列1,2,3,4,…,500中去除一些数,组成一个新数列,要求这个新数列中的任意两个数之和都不是7的倍数,则这个新数列中最大的数是( )
| A、216 | B、217 |
| C、213 | D、287 |
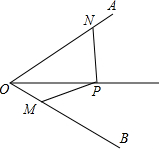 如图,已知点P在∠AOB的平分线上,且∠ONP+∠OMP=180°,求证:PM=PN.
如图,已知点P在∠AOB的平分线上,且∠ONP+∠OMP=180°,求证:PM=PN.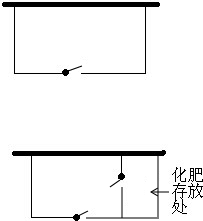 张大爷用32米长的篱笆围成一个矩形菜园,菜园一边靠墙(墙长为15米),平行于墙的一面开一扇宽度为2米的门(如图1).(注:门都用其它材料)
张大爷用32米长的篱笆围成一个矩形菜园,菜园一边靠墙(墙长为15米),平行于墙的一面开一扇宽度为2米的门(如图1).(注:门都用其它材料)