题目内容
16.计算或化简:(1)($\frac{1}{3}$)-1-20140-|-2|+tan45°
(2)(1+$\frac{3}{a-2}$)÷$\frac{a+1}{{a}^{2}-4}$.
分析 (1)本题涉及负整数指数幂、零指数幂、绝对值、特殊角的三角函数值4个考点.在计算时,需要针对每个考点分别进行计算,然后根据实数的运算法则求得计算结果.
(2)先通分计算括号里面的除法,再将除法变为乘法,约分计算即可求解.
解答 解:(1)($\frac{1}{3}$)-1-20140-|-2|+tan45°
=3-1-2+1
=1;
(2)(1+$\frac{3}{a-2}$)÷$\frac{a+1}{{a}^{2}-4}$
=$\frac{a-2+3}{a-2}$×$\frac{(a+2)(a-2)}{a+1}$
=$\frac{a+1}{a-2}$×$\frac{(a+2)(a-2)}{a+1}$
=a+2.
点评 本题主要考查了实数的综合运算能力,是各地中考题中常见的计算题型.解决此类题目的关键是熟练掌握负整数指数幂、零指数幂、绝对值、特殊角的三角函数值等考点的运算.同时考查了分式的化简求值,熟练掌握运算法则是解本题的关键.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案
相关题目
4.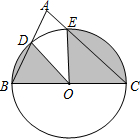 如图,以BC为直径的半圆⊙O与△ABC的边AB、AC分别相交于点D、E.若∠A=80°,BC=4,则图中阴影部分图形的面积和为( )
如图,以BC为直径的半圆⊙O与△ABC的边AB、AC分别相交于点D、E.若∠A=80°,BC=4,则图中阴影部分图形的面积和为( )
 如图,以BC为直径的半圆⊙O与△ABC的边AB、AC分别相交于点D、E.若∠A=80°,BC=4,则图中阴影部分图形的面积和为( )
如图,以BC为直径的半圆⊙O与△ABC的边AB、AC分别相交于点D、E.若∠A=80°,BC=4,则图中阴影部分图形的面积和为( )| A. | $\frac{64}{9}π$ | B. | $\frac{32}{9}π$ | C. | $\frac{16}{9}π$ | D. | $\frac{8}{9}π$ |
5.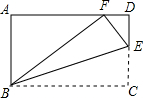 如图,在矩形ABCD中,AB=3,BC=5,点E在边CD上,连接BE,将△BCE沿BE折叠,若点C恰好落在AD边上的点F处,则CE的长为( )
如图,在矩形ABCD中,AB=3,BC=5,点E在边CD上,连接BE,将△BCE沿BE折叠,若点C恰好落在AD边上的点F处,则CE的长为( )
 如图,在矩形ABCD中,AB=3,BC=5,点E在边CD上,连接BE,将△BCE沿BE折叠,若点C恰好落在AD边上的点F处,则CE的长为( )
如图,在矩形ABCD中,AB=3,BC=5,点E在边CD上,连接BE,将△BCE沿BE折叠,若点C恰好落在AD边上的点F处,则CE的长为( )| A. | $\frac{3}{5}$ | B. | $\frac{5}{3}$ | C. | $\frac{3}{4}$ | D. | $\frac{4}{3}$ |
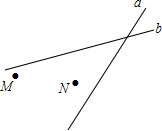 如图:某地有两所大学M、N和两条相交叉的公路a、b,现计划修建一座物资仓库,希望仓库到两所大学的距离相等,到两条公路的距离也相等.你能确定仓库应该建在什么位置吗?在所给的图形中画出你的设计方案.
如图:某地有两所大学M、N和两条相交叉的公路a、b,现计划修建一座物资仓库,希望仓库到两所大学的距离相等,到两条公路的距离也相等.你能确定仓库应该建在什么位置吗?在所给的图形中画出你的设计方案. 甲、乙两车从A地驶向B地,甲车比乙车早行驶2h,并且在途中休息了0.5h,休息前后速度相同,如图是甲、乙两车行驶的距离y(km)与时间x(h)的函数图象.
甲、乙两车从A地驶向B地,甲车比乙车早行驶2h,并且在途中休息了0.5h,休息前后速度相同,如图是甲、乙两车行驶的距离y(km)与时间x(h)的函数图象.
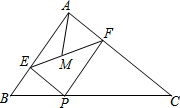 如图,在Rt△ABC中,∠BAC=90°,AB=6,AC=8,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,M为EF中点,则AM的最小值是$\frac{12}{5}$.
如图,在Rt△ABC中,∠BAC=90°,AB=6,AC=8,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,M为EF中点,则AM的最小值是$\frac{12}{5}$.