题目内容
20．
如图，过反比例函数y=$\frac{3}{x}$（x＞0）图象上任意两点A、B分别作x轴的垂线，垂足为C、D，连接OA、OB．设AC与OB的交点为E，△AOE与梯形ECDB的面积分别为S1、S2，则（ ）| A． | S1＞S2 | B． | S1=S2 | ||
| C． | S1＜S2 | D． | S1、S2的大小关系不确定 |
分析 根据反比例函数比例系数k的几何意义即可判断．
解答 解：∵S△AOC=S△OBD，
即S△AOE+S△OEC=S△OEC+S梯形ECDB，
∴S△AOE=S梯形ECDB．即S1=S2．
故选B．
点评 本题主要考查反比例函数系数k的几何意义，反比例函数$y=\frac{k}{x}$中k的几何意义，即过双曲线上任意一点引x轴、y轴垂线，所得矩形面积为|k|，是经常考查的一个知识点；这里体现了数形结合的思想，做此类题一定要正确理解k的几何意义．
练习册系列答案
名校课堂系列答案
相关题目
10．
如图，CD=CE，AE=BD，∠ADC=∠BEC=100°，∠ACD=26°，则∠BCD的度数是（ ）
如图，CD=CE，AE=BD，∠ADC=∠BEC=100°，∠ACD=26°，则∠BCD的度数是（ ）| A． | 72° | B． | 54° | C． | 46° | D． | 20° |
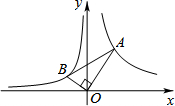如图，已知第一象限内的点A在反比例函y=$\frac{4}{x}$上，第二象限的点B在反比例函数y=$\frac{k}{x}$上，且OA⊥OB，tanA=$\frac{1}{2}$，则k的值为-1．
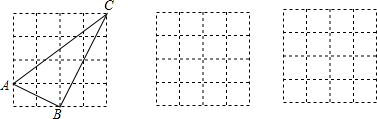
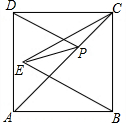如图，正方形ABCD的边长为8，△BCE是等边三角形，点E在正方形内，在对角线AC上有一点P，使PD+PE的和最小，则这个最小值为（ ）
如图，△ABC中，∠1=∠2，∠ABC=∠C，∠4=∠5，求∠5的度数．