题目内容
12. 如图,AB、CD为两个建筑物,建筑物AB的高度为60米,从建筑物AB的顶点A处测得建筑物CD的顶点C的俯角∠EAC=30°,测得底部D点的俯角∠EAD=45°.
如图,AB、CD为两个建筑物,建筑物AB的高度为60米,从建筑物AB的顶点A处测得建筑物CD的顶点C的俯角∠EAC=30°,测得底部D点的俯角∠EAD=45°.(1)求两建筑物之间水平距离BD的长度;
(2)求建筑物CD的高度(结果保留根号).
分析 (1)根据题意得:BD∥AE,从而得到∠BAD=∠ADB=45°,利用BD=AB=60,求得两建筑物底部之间水平距离BD的长度为60米;
(2)延长AE、DC交于点F,根据题意得四边形ABDF为正方形,根据AF=BD=DF=60,在Rt△AFC中利用∠FAC=30°求得CF,然后即可求得CD的长.
解答 解:(1)根据题意得:BD∥AE,
∴∠ADB=∠EAD=45°,
∵∠ABD=90°,
∴∠BAD=∠ADB=45°,
∴BD=AB=60米,
答:两建筑物底部之间水平距离BD的长度为60米;
(2)延长AE、DC交于点F,根据题意得四边形ABDF为正方形,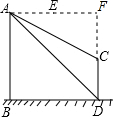
∴AF=BD=DF=60米,
在Rt△AFC中,∠FAC=30°,
∴CF=AF•tan∠FAC=60×$\frac{\sqrt{3}}{3}$=20$\sqrt{3}$米,
又∵FD=60米,
∴CD=60-20$\sqrt{3}$(米).
答:建筑物CD的高度为(60-20$\sqrt{3}$)米.
点评 本题考查的是解直角三角形的应用-仰角俯角问题,正确标注仰角和俯角、熟记锐角三角函数的定义是解题的关键.

练习册系列答案
相关题目
3.2015年十一国庆长假提前到9月29日,黄金周期间外出旅游更为火爆,若旅游区的门票为60元/张,某旅游区的开放时间为每天10小时,并每小时对进入旅游区的游客人数进行一次统计,下表是9月30日对进入旅游区人数的7次抽样统计数据:
那么从9月29日至10月5日旅游区门票收入是多少?( )
| 记数的次数 | 第1次 | 第2次 | 第3次 | 第4次 | 第5次 | 第6次 | 第7次 |
| 每小时进入旅游区的人数 | 318 | 310 | 310 | 286 | 280 | 312 | 284 |
| A. | 900000元 | B. | 1260000元 | C. | 191600元 | D. | 162000元 |
7.下列结论中正确的是( )
| A. | a3+a2=a5 | B. | a3•a2=a6 | C. | a3÷a2=a | D. | (a3)2=a5 |
 如图,在△ABC中,E为AB边上的一点,要使△ABC∽△ADE成立,还需要添加一个条件为∠ADE=∠B(答案不唯一).
如图,在△ABC中,E为AB边上的一点,要使△ABC∽△ADE成立,还需要添加一个条件为∠ADE=∠B(答案不唯一).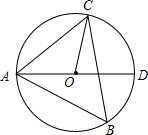 如图,△ABC内接于⊙O,AD是直径,sinB=$\frac{5}{34}$$\sqrt{34}$.
如图,△ABC内接于⊙O,AD是直径,sinB=$\frac{5}{34}$$\sqrt{34}$.